005-分类算法
分类算法
DNN二分类
深度神经网络(DNN)是多层功能神经元模型,每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接,其中输入层神经元接受外界输入,隐层与输出层神经元对信号进行加工,最终结果由输出层神经元输出,换言之,输入层神经元仅是接受输入,不进行函数处理,隐层与输出层包含功能神经元。神经网络的学习过程,就是根据训练数据来调整神经元之间的连接权以及每个功能神经元的阈值,换言之,神经网络学到的东西,蕴涵在连接权与阈值中。 神经元模型:神经元接受到来自 n 个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接受到的总输入值将与神经元的阈值进行比较,然后通过激活函数处理以产生神经元的输出。 学习算法:误差逆传播算法, DNN 二分类:输出层神经元完成二分类任务。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int,标记列必须是String或Int类型(如果列中的unique值超过了两种,运行算子时会报错)。
输出
- 输出DNN二分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 隐藏层节点数 | 是 | 隐藏层节点数,数组中必须为正整数 范围:[1, inf)。 | 10 |
| 数据块大小 | 否 | 用于设置在矩阵中堆叠输入数据的块大小以加速计算 范围:[1, 1000]。 | 128 |
| 优化方法 | 是 | 优化方法支持 gd(minibatch gradient descent) 或 l-bfgs。 | l-bfgs |
| 迭代步长 | 是 | 每次优化的迭代步长,仅适用于gd 范围:[1.0E-12, inf)。 | 0.03 |
| 最大迭代次数 | 是 | 最大迭代次数,默认迭代100次 范围:[0, inf)。 | 100 |
| 收敛容差 | 是 | 迭代时的收敛容差 范围:[0.0, inf)。 | 1e-6 |
| 随机种子 | 是 | 随机种子 | 1 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列。要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 真实标签列。要求不是数组类型,唯一值是2。 | 无 |
| 正样本标签值 | 否 | 二分类的正样本的标签值,应在标签列中存在。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| 最大迭代次数 | 是 | 最大迭代次数,默认迭代100次 范围:[0, inf)。 | 100 |
| 评估标准 | 是 | 选择评估标准: 准确率 pr曲线下面积 roc曲线下面积 F1分数 精确率 召回率 |
roc曲线下面积 |
| 保存模型数量 | 是 | 保存模型的数量。 | 1 |
使用示例
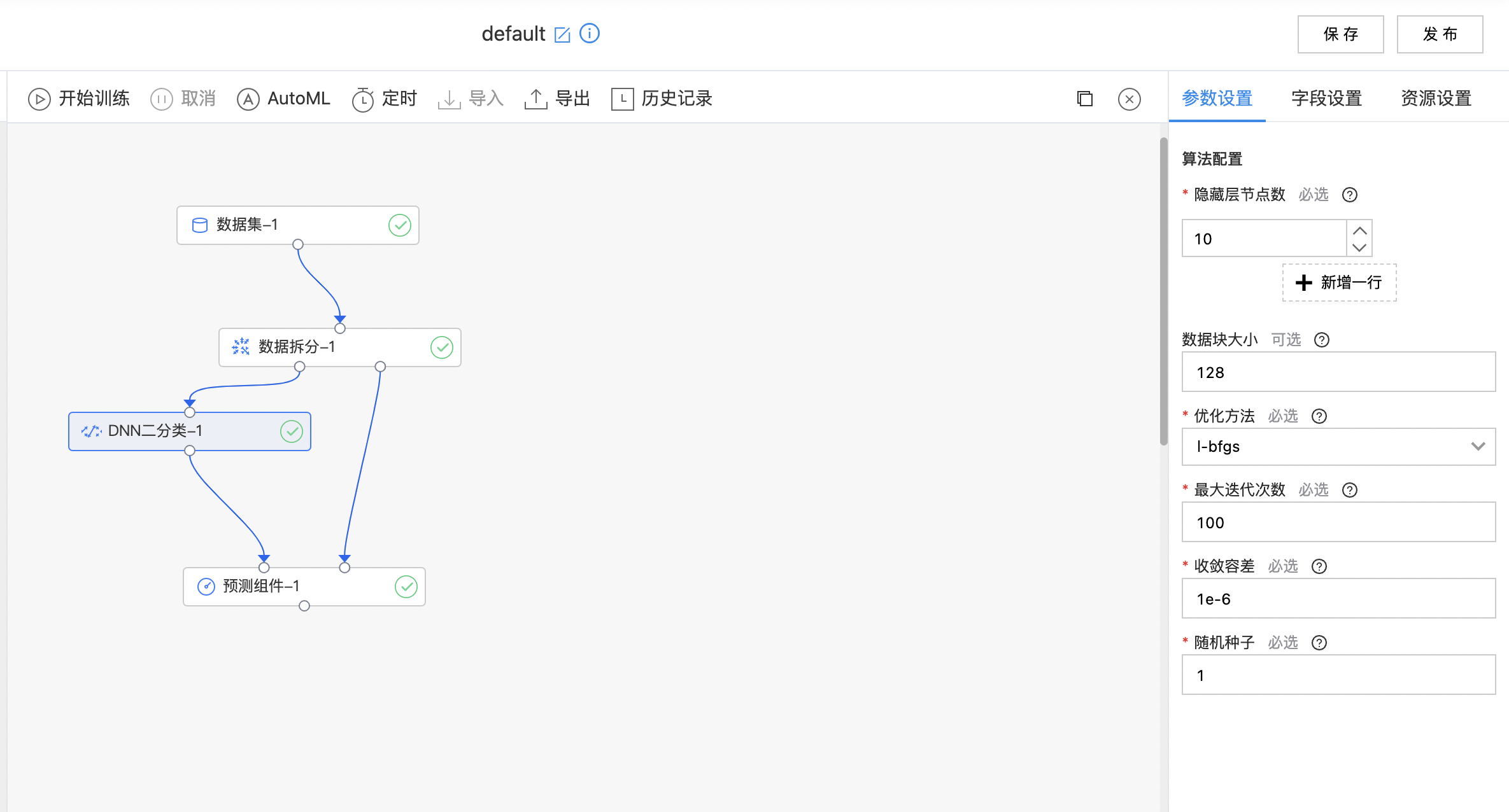
- 构建算子结构,配置模型参数,完成训练。
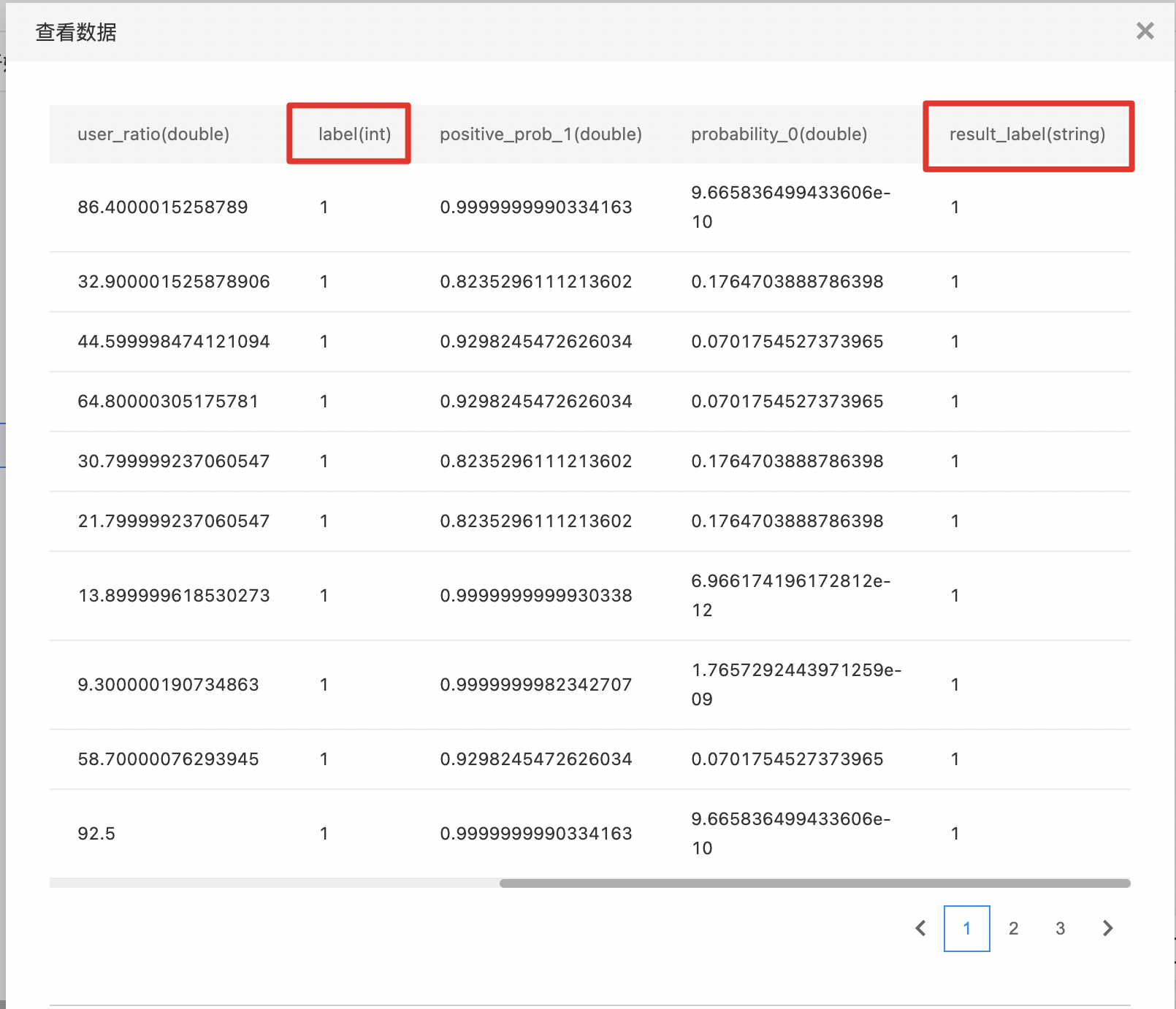
- 查看预测结果。
DNN多分类
深度神经网络(DNN)多分类是基于多层功能神经元模型的多分类模型,其中输出层神经元完成多分类任务。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int,标记列必须是String或Int类型(列中的unique值超过两种)。
输出
- 输出DNN多分类模型,支持查看Top10分类的概率。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 隐藏层节点数 | 是 | 隐藏层节点数,数组中必须为正整数 范围:[1, inf)。 | 10 |
| 数据块大小 | 否 | 用于设置在矩阵中堆叠输入数据的块大小以加速计算 范围:[1, 1000]。 | 128 |
| 优化方法 | 是 | 优化方法支持 gd(minibatch gradient descent) 或 l-bfgs。 | l-bfgs |
| 迭代步长 | 是 | 每次优化的迭代步长,仅适用于gd 范围:[1.0E-12, inf)。 | 0.03 |
| 最大迭代次数 | 是 | 最大迭代次数,默认迭代100次 范围:[0, inf)。 | 100 |
| 收敛容差 | 是 | 迭代时的收敛容差 范围:[0.0, inf)。 | 1e-6 |
| 随机种子 | 是 | 随机种子 | 1 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 真实标签列。当数据量或标签数量过大时,需增加内存。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| 最大迭代次数 | 是 | 最大迭代次数,默认迭代100次 范围:[0, inf)。 | 100 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量。 | 1 |
使用示例
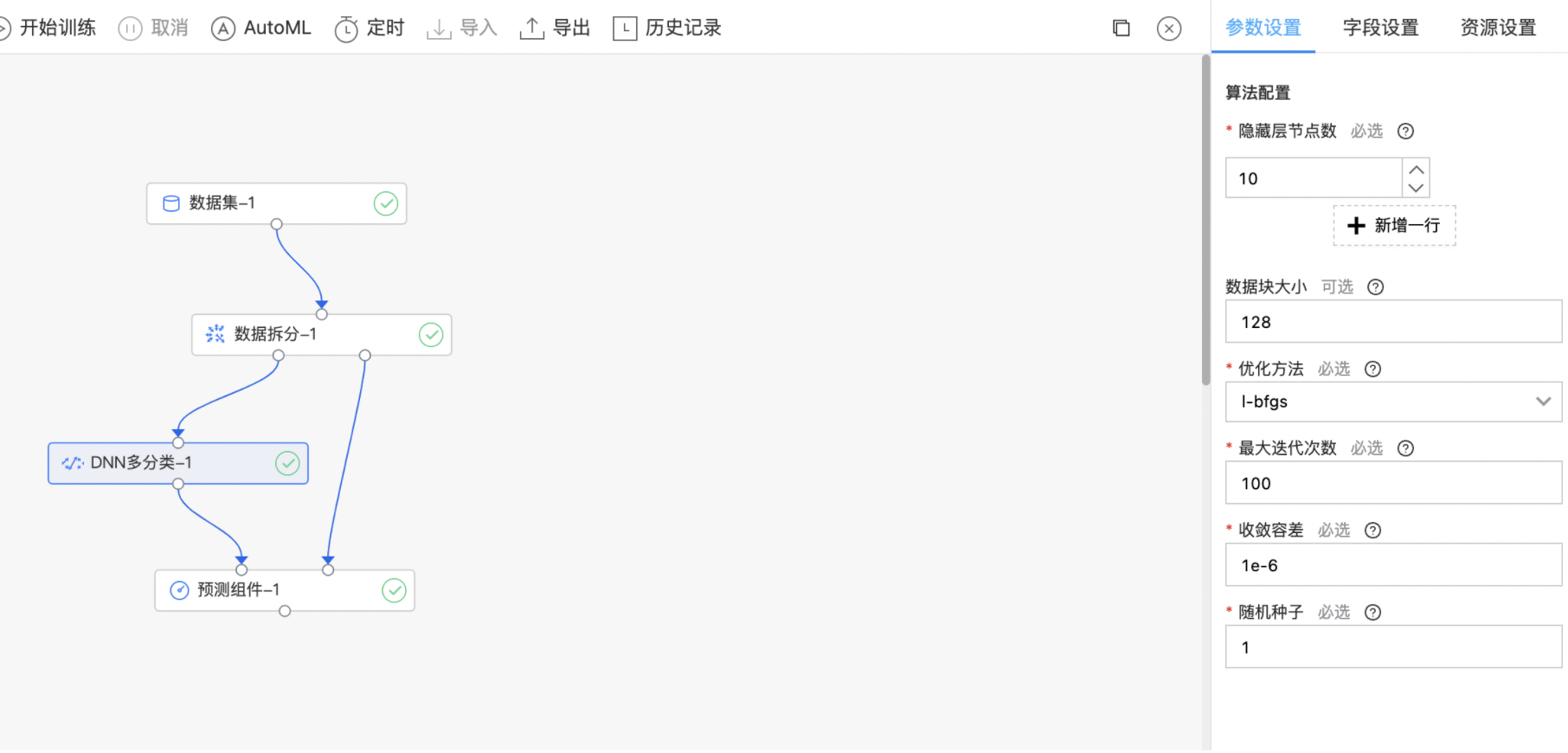
构建算子结构,配置参数,完成训练。
DecisionTree二分类
决策树(DecisionTree)是一类常见的机器学习方法。它从给定训练数据集学得一个模型用以对新示例进行分类。二分类的任务,可看作对“当前样本属于正类吗?”这个问题的“决策”或“判定”过程。决策树是基于树结构来进行决策的。 决策树学习的关键是如何选择最优划分属性。一般而言,随着划分过程不断进行,决策树分支结点的“纯度”越来越高。
输入
- 输入一个数据集,数据集的特征列double/int,标记列是String或Int类型,标记列唯一值是2。
输出
- 输出DecisionTree二分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 树最大深度 | 是 | 决策树最大深度 范围:[0, 30]。 | 5 |
| 连续特征分箱数 | 是 | 决策树连续特征分箱数 范围:[2, inf)。 | 32 |
| 分裂指标 | 是 | 分裂指标: gini-基尼系数 entropy-熵 计算公式可查看【特征自动选择】组件 |
gini |
| 最小信息增益 | 是 | 决策树分裂时最小信息增益 范围:[0.0, inf)。 | 0 |
| 节点最小样本数 | 是 | 决策树节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf)。 | 5 |
| 随机种子 | 否 | 随机种子 | 5 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 真实标签列。要求不是数组类型,唯一值是2。 | 无 |
| 正样本标签值 | 否 | 二分类的正样本的标签值,应在标签列中存在。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| 树最大深度 | 是 | 决策树最大深度 范围:[0, 30]。 | 5 |
| 连续特征分箱数 | 是 | 决策树连续特征分箱数 范围:[2, inf)。 | 32 |
| 节点最小样本数 | 是 | 决策树节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf)。 | 5 |
| 最小信息增益 | 是 | 决策树分裂时最小信息增益 范围:[0.0, inf)。 | 0 |
| 评估标准 | 是 | 选择评估标准: 准确率 pr曲线下面积 roc曲线下面积 F1分数 精确率 召回率 |
roc曲线下面积 |
| 保存模型数量 | 是 | 保存模型的数量。 | 1 |
使用示例
构建算子结构,配置参数,完成训练。
DecisionTree多分类
决策树(DecisionTree)多分类是基于树结构对于多分类任务进行决策,原理和划分选择与二分类一样。
输入
- 输入一个数据集,数据集的特征列double/int,标记列是String或Int类型,标记列唯一值>=3。
输出
- 输出DecisionTree多分类模型,支持查看Top10分类的概率。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 树最大深度 | 是 | 决策树最大深度 范围:[0, 30] | 5 |
| 连续特征分箱数 | 是 | 决策树连续特征分箱数 范围:[2, inf) | 32 |
| 分裂指标 | 是 | 分裂指标: gini entropy |
gini |
| 最小信息增益 | 是 | 决策树分裂时最小信息增益 范围:[0.0, inf) | 0 |
| 节点最小样本数 | 是 | 决策树节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf) | 5 |
| 随机种子 | 否 | 随机种子 | 5 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求不是数组类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 树最大深度 | 是 | 决策树最大深度 范围:[0, 30] | 5 |
| 连续特征分箱数 | 是 | 决策树连续特征分箱数 范围:[2, inf) | 32 |
| 节点最小样本数 | 是 | 决策树节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf) | 5 |
| 最小信息增益 | 是 | 决策树分裂时最小信息增益 范围:[0.0, inf) | 0 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
使用示例
构建算子结构,配置参数,完成训练。
逻辑回归二分类
经典逻辑回归是一个二分类算法。它通过对数几率函数(logistic function)将线性回归模型产生的预测值转化为一个接近 0 或 1 的值。组件支持稠密数据格式。逻辑回归实现分类的思想:将每条样本进行打分,然后设置一个阈值,达到这个阈值的,分为一个类别,没有达到这个阈值的,分为另外一个类别。对于阈值,划分为哪个类别都可以,但是,要保证阈值划分的一致性。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int,标记列必须是String或Int类型(如果列中的unique值超过了两种,运行算子时会报错)。
输出
- 输出逻辑回归二分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| alpha | 是 | 正则项的选择,alpha=0代表L2正则,alpha=1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0] | 0.00 |
| lambda | 是 | 正则项的系数,0代表没有正则,越大代表正则强度越大 范围:[0.0, 2.0] | 1 |
| 随机种子 | 否 | 随机种子,用于保证多次训练结果相同 | 无 |
| 最大迭代轮数 | 否 | 最大迭代轮数 范围:[1, 1000] | 20 |
| 目标收敛阈值 | 否 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练。默认值1e-6 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
| 是否交叉验证 | 是 | 是否进行交叉验证 | 否 |
| 交叉验证份数 | 是 | 交叉验证的份数 范围:[2, 20] | 5 |
| 交叉验证划分方式 | 是 | 交叉验证每份的划分方式。选择分层划分的话,是按照分类目标列分层划分。目前支持:随机划分、分层划分、取余划分。 | 随机划分 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列。要求必须是数值或数值数组类型 | 无 |
| 标签列 | 是 | 真实标签列。要求不是数组类型,唯一值是2 | 无 |
| 正样本标签值 | 否 | 二分类的正样本的标签值,应在标签列中存在 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| alpha | 是 | 正则项的选择,alpha=0代表L2正则,alpha=1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0] | 0 |
| lambda | 是 | 正则项的系数,0代表没有正则,越大代表正则强度越大 范围:[0.0, 2.0] | 1 |
| 最大迭代轮数 | 是 | 最大迭代轮数 范围:[1, 1000] | 20 |
| 目标收敛阈值 | 是 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练。默认值1e-6 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
| 评估标准 | 是 | 选择评估标准: 准确率 pr曲线下面积 roc曲线下面积 F1分数 精确率 召回率 |
roc曲线下面积 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
计算逻辑
逻辑回归二分类模型(Sigmoid函数):

L1正则是指权值向量中各个元素的绝对值之和。
L2正则是指权值向量中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号)。
使用示例
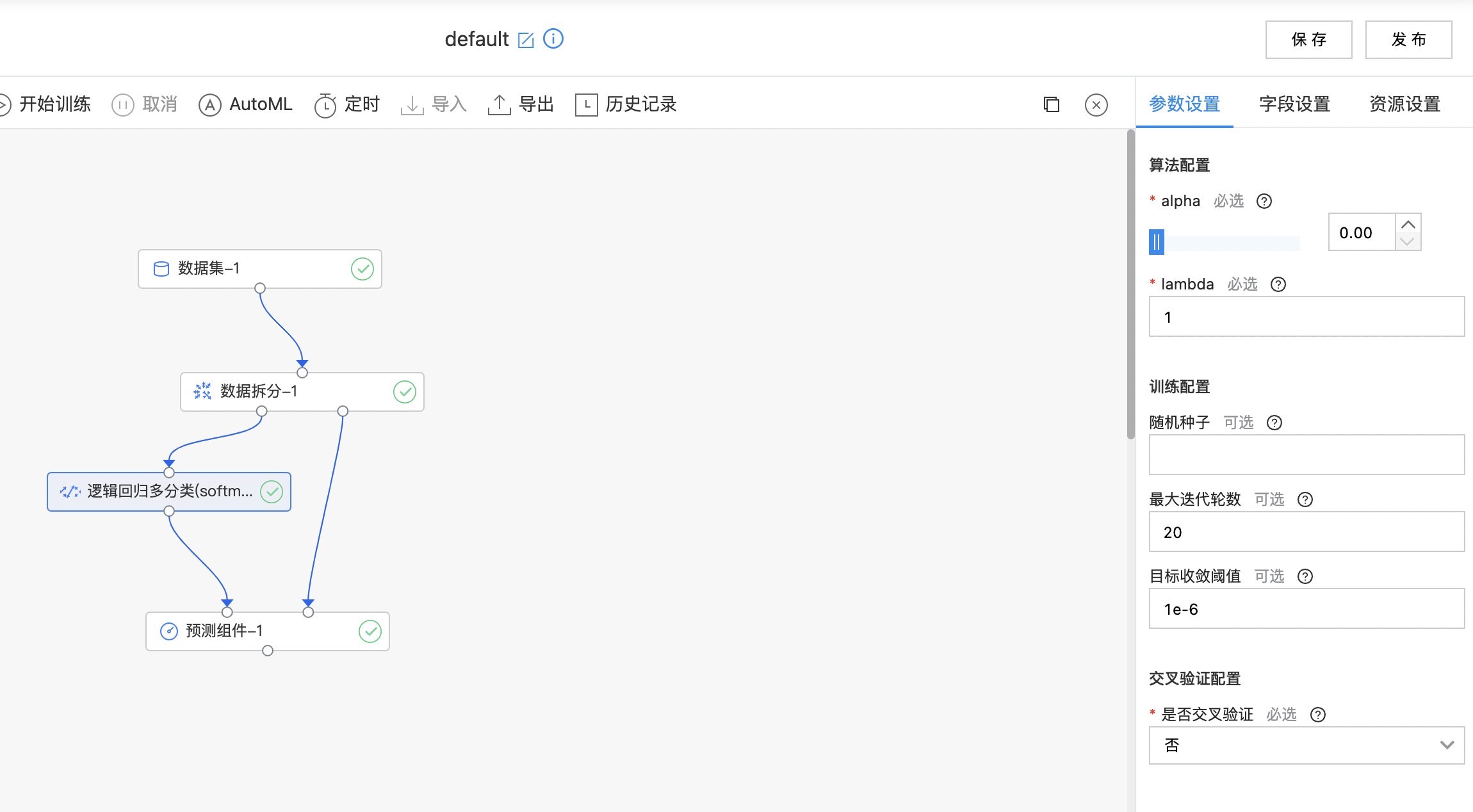
构建如下图算子结构,配置算子参数后开始训练。
逻辑回归多分类(softmax)
经典逻辑回归的推广,是一个多分类算法。它通过 softmax 函数将线性回归模型产生的预测值转化为多个接近 0 或 1 的值。组件支持稠密数据格式。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int。
输出
- 输出逻辑回归多分类模型,支持查看Top10分类的概率。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| alpha | 是 | 正则项的选择,alpha=0代表L2正则,alpha=1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0] | 0.00 |
| lambda | 是 | 正则项的系数,0代表没有正则,越大代表正则强度越大 范围:[0.0, 2.0] | 1 |
| 随机种子 | 否 | 随机种子,用于保证多次训练结果相同 | 无 |
| 最大迭代轮数 | 否 | 最大迭代轮数 范围:[1, 1000] | 20 |
| 目标收敛阈值 | 否 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练。默认值1e-6 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
| 是否交叉验证 | 是 | 是否进行交叉验证 | 否 |
| 交叉份数 | 是 | 交叉验证的份数 范围:[2, 20] | 5 |
| 交叉验证划分方式 | 是 | 交叉验证每份的划分方式。选择分层划分的话,是按照分类目标列分层划分 | 随机划分 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 标签列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型 | 无 |
| 特征列 | 是 | 交叉验证每份的划分方式。选择分层划分的话,是按照分类目标列分层划分。目前支持:随机划分、分层划分、取余划分。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| alpha | 是 | 正则项的选择,alpha=0代表L2正则,alpha=1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0] | 0 |
| lambda | 是 | 正则项的系数,0代表没有正则,越大代表正则强度越大 范围:[0.0, 2.0] | 1 |
| 最大迭代轮数 | 是 | 最大迭代轮数 范围:[1, 1000] | 20 |
| 目标收敛阈值 | 是 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练。默认值1e-6 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
计算逻辑
逻辑回归多分类(k 类)模型:
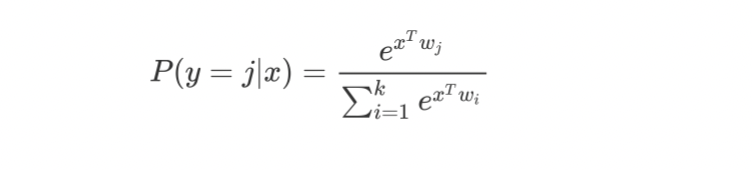
使用示例
构建算子结构,配置参数,完成训练。
朴素贝叶斯二分类
朴素贝叶斯是一种简单的概率分类器,它基于贝叶斯定理应用特征之间的强独立假设(属性条件独立性假设)。朴素贝叶斯二分类对应于二分类任务。 朴素贝叶斯的一个优点是它只需要少量的训练数据来估计分类所需的参数。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int,标记列必须是String或Int类型(如果列中的unique值超过了两种,运行算子时会报错)。
输出
- 输出朴素贝叶斯二分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 模型 | 是 | 贝叶斯分类模型。如果使用伯努利模型,需要保证每个特征列都是0-1变量;如果使用多项式模型,需要保证每个特征列都是非负值。 | 多项式模型 |
| 平滑参数 | 是 | 平滑参数越大模型越平滑,不容易过拟合 范围:[0.0, inf) | 1.0 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列。要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 真实标签列。要求不是数组类型,唯一值是2。 | 无 |
| 正样本标签值 | 否 | 二分类的正样本的标签值,应在标签列中存在。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 平滑参数 | 是 | 平滑参数越大模型越平滑,不容易过拟合 范围:[0.0, inf | 1.0 |
| 评估标准 | 是 | 选择评估标准: 准确率 pr曲线下面积 roc曲线下面积 F1分数 精确率 召回率 |
roc曲线下面积 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
计算逻辑
朴素贝叶斯分类器:

多项式模型:
当特征是离散的时候,使用多项式模型。多项式模型在计算先验概率和条件概率时,会做一些平滑处理。如果不做平滑,当某一维特征的值没在训练样本中出现过时,会导致条件概率值为0,从而导致后验概率为0,加上平滑就可以克服这个问题。

伯努利模型:
与多项式模型一样,伯努利模型适用于离散特征的情况,所不同的是,伯努利模型中每个特征的取值只能是1和0(以文本分类为例,某个单词在文档中出现过,则其特征值为1,否则为0)。
伯努利模型中,条件概率的计算方式是:
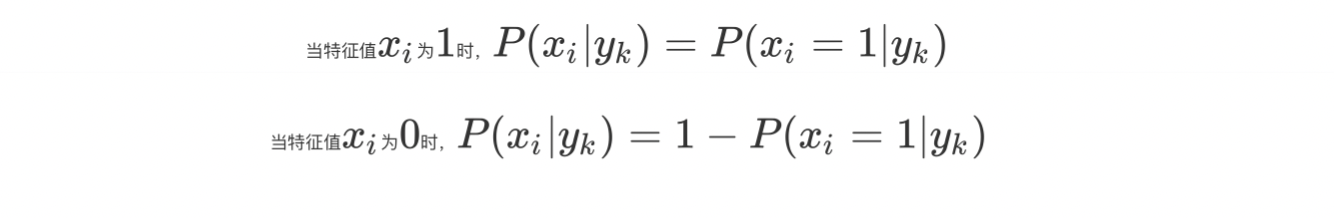
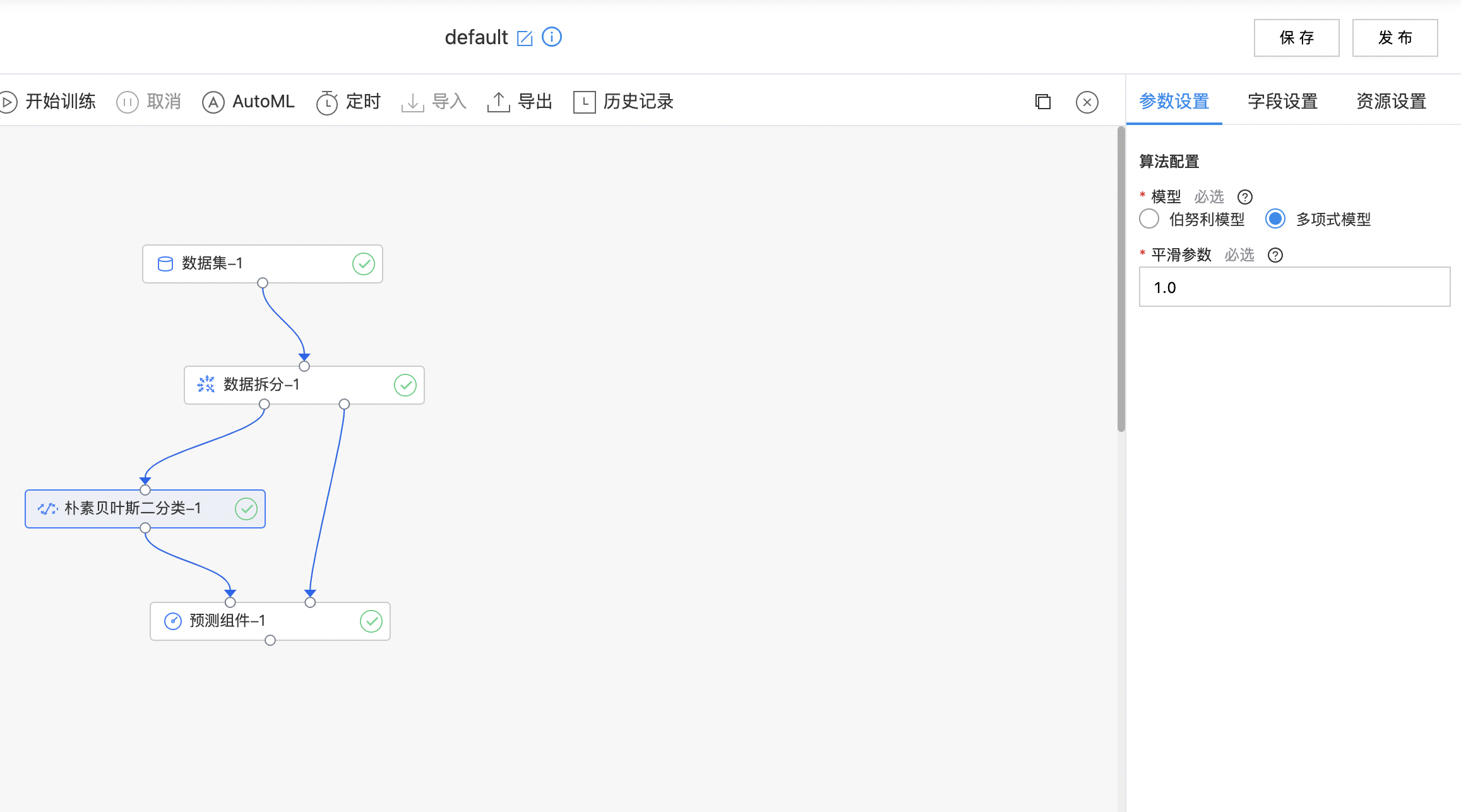
使用示例
构建算子结构,配置参数,完成训练。
朴素贝叶斯多分类
朴素贝叶斯多分类是基于贝叶斯定理以及属性条件独立性假设得到的多分类模型,原理与二分类一样。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int。
输出
- 输出朴素贝叶斯多分类模型,支持查看Top10分类的概率。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 模型 | 是 | 贝叶斯分类模型。如果使用伯努利模型,需要保证每个特征列都是0-1变量;如果使用多项式模型,需要保证每个特征列都是非负值。 | 多项式模型 |
| 平滑参数 | 是 | 平滑参数越大模型越平滑,不容易过拟合 范围:[0.0, inf) | 1.0 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型 | 无 |
| 标签列 | 是 | 预测目标列,要求不是数组类型。当数据量或标签数量过大时,需增加内存。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 平滑参数 | 是 | 平滑参数越大模型越平滑,不容易过拟合 范围:[0.0, inf | 1.0 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
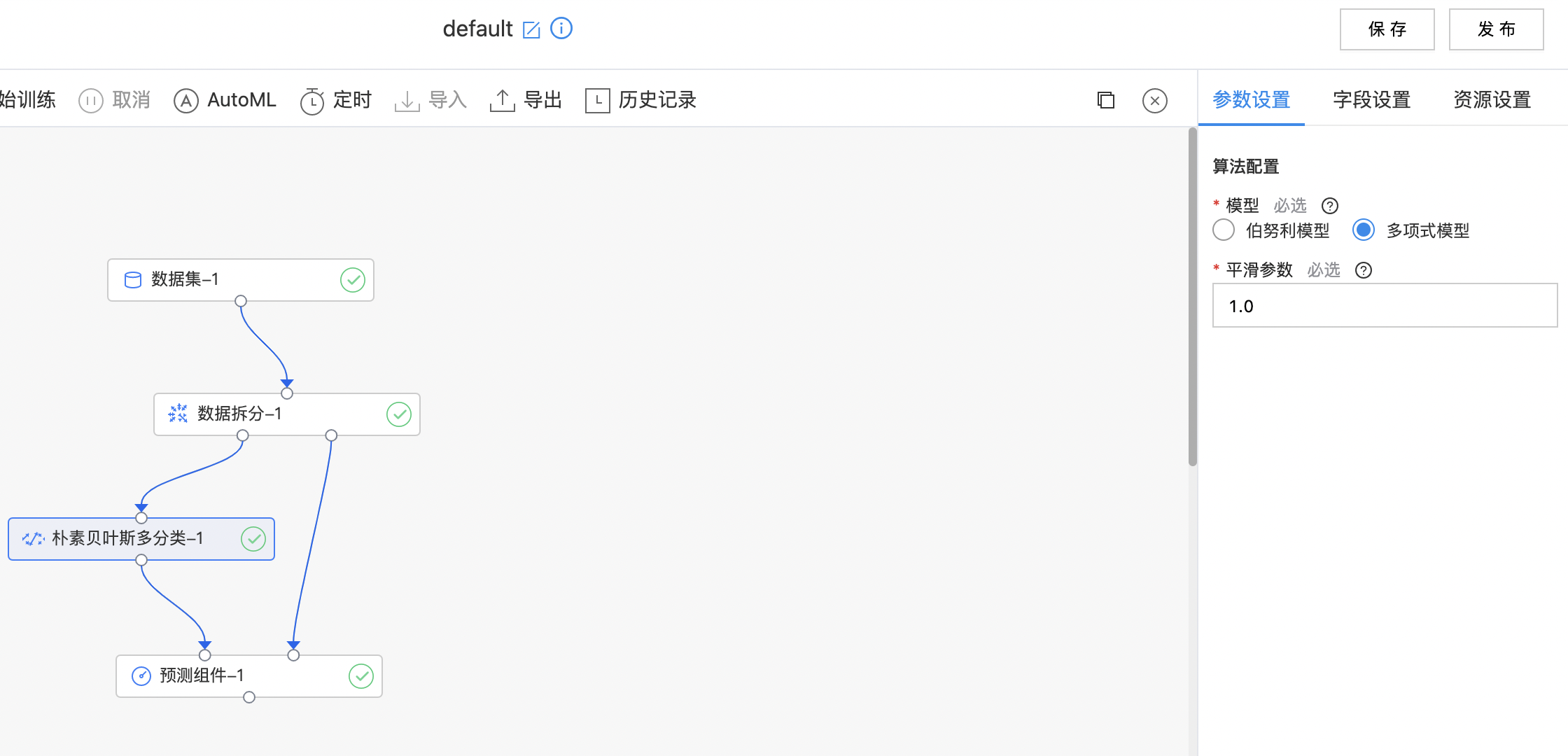
使用示例
构建算子结构,配置参数,完成训练。
随机森林二分类
随机森林(RF)是 Bagging(并行式集成学习方法) 的一个扩展变体。RF 在以决策树为基学习器构建 Bagging 集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。具体来说,传统决策树在选择划分属性时是在当前结点的属性集合(假定有 d 个属性)中选择一个最优属性;而在 RF 中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含 k 个属性的子集,然后再从这个子集中选择一个最优属性用于划分。随机森林二分类对应于二分类任务。基学习器为 DecisionTree 二分类。结合策略是使用投票法。 随机森林简单、容易实现、计算开销小,它在很多现实任务中展现出强大的性能。
输入
- 输入一个数据集,数据集的特征列double/int,标记列是String或Int类型,标记列唯一值是2。
输出
- 输出随机森林二分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征采样策略 | 是 | 每次分裂子树时,考虑多少个特征,支持以下策略: 所有特征 自动选择 总特证数以二为底的对数 定值 三分之一的特征 总特征数的一定比例 总特征数的平方根 |
自动选择 |
| 特征采样数 | 是 | 每次分裂子树时,考虑多少个特征 范围:[1, inf) | 10 |
| 信息增益计算 | 是 | 分裂时计算子节点信息增益的策略,目前支持:信息熵、基尼不纯度。 | 基尼不纯度 |
| 树的最大深度 | 是 | 树的最大深度,范围:[2, 30] | 5 |
| 最小信息增益 | 是 | 每次分裂所需的最小信息增益 范围:[0.0, inf) | 0.0 |
| 节点最小样本数 | 是 | 节点最小的样本数,范围:[1, inf) | 1 |
| 树的数量 | 是 | 子树的数量,范围:[1, inf) | 20 |
| 随机种子 | 是 | 随机种子 | 1 |
| 采样率 | 是 | 训练每个子树时,使用的样本占总样本的比例。采样率不宜过小,至少应当保证(训练样本数*采样率>1),否则训练出的模型在预测时会报错 Can not normalize the 0-vector. 范围:[0.001, 0.999] | 0.632 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列。要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 真实标签列。要求不是数组类型,唯一值是2。 | 无 |
| 正样本标签值 | 否 | 二分类的正样本的标签值,应在标签列中存在。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 树的最大深度 | 是 | 最大迭代次数,默认迭代100次 范围:[0, inf) | 5 |
| 最小信息增益 | 是 | 每次分裂所需的最小信息增益 范围:[0.0, inf) | 0.0 |
| 节点最小样本数 | 是 | 节点最小的样本数,范围:[1, inf) | 1 |
| 树的数量 | 是 | 子树的数量,范围:[1, inf) | 20 |
| 采样率 | 是 | 训练每个子树时,使用的样本占总样本的比例。采样率不宜过小,至少应当保证(训练样本数*采样率>1),否则训练出的模型在预测时会报错 Can not normalize the 0-vector. 范围:[0.001, 0.999] | 0.632 |
| 评估标准 | 是 | 选择评估标准: 准确率 pr曲线下面积 roc曲线下面积 F1分数 精确率 召回率 |
roc曲线下面积 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
计算逻辑
基尼不纯度:从一个数据集中随机选取子项,度量其被错误的划分到其他组里的概率,也就是一个随机事件变成它的对立事件的概率。
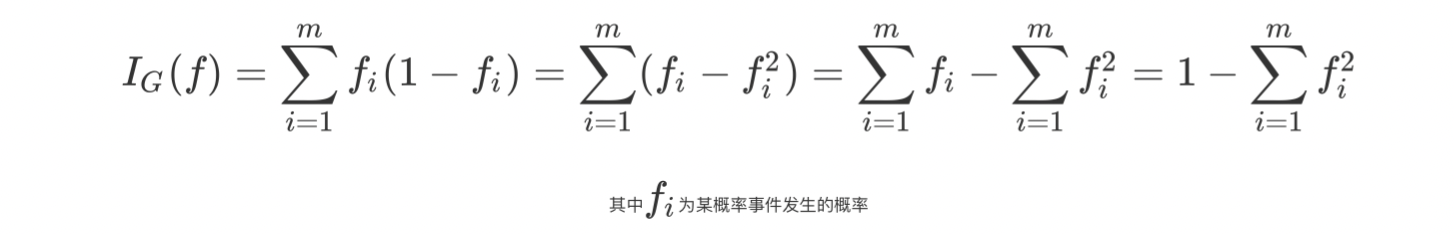
可见,基尼不纯度可以作为衡量系统混乱程度的标准;基尼不纯度越小,纯度越高,集合的有序程度越高,分类的效果越好;基尼不纯度为 0 时,表示集合类别一致;在决策树中,比较基尼不纯度的大小可以选择更好的决策条件(子节点)。
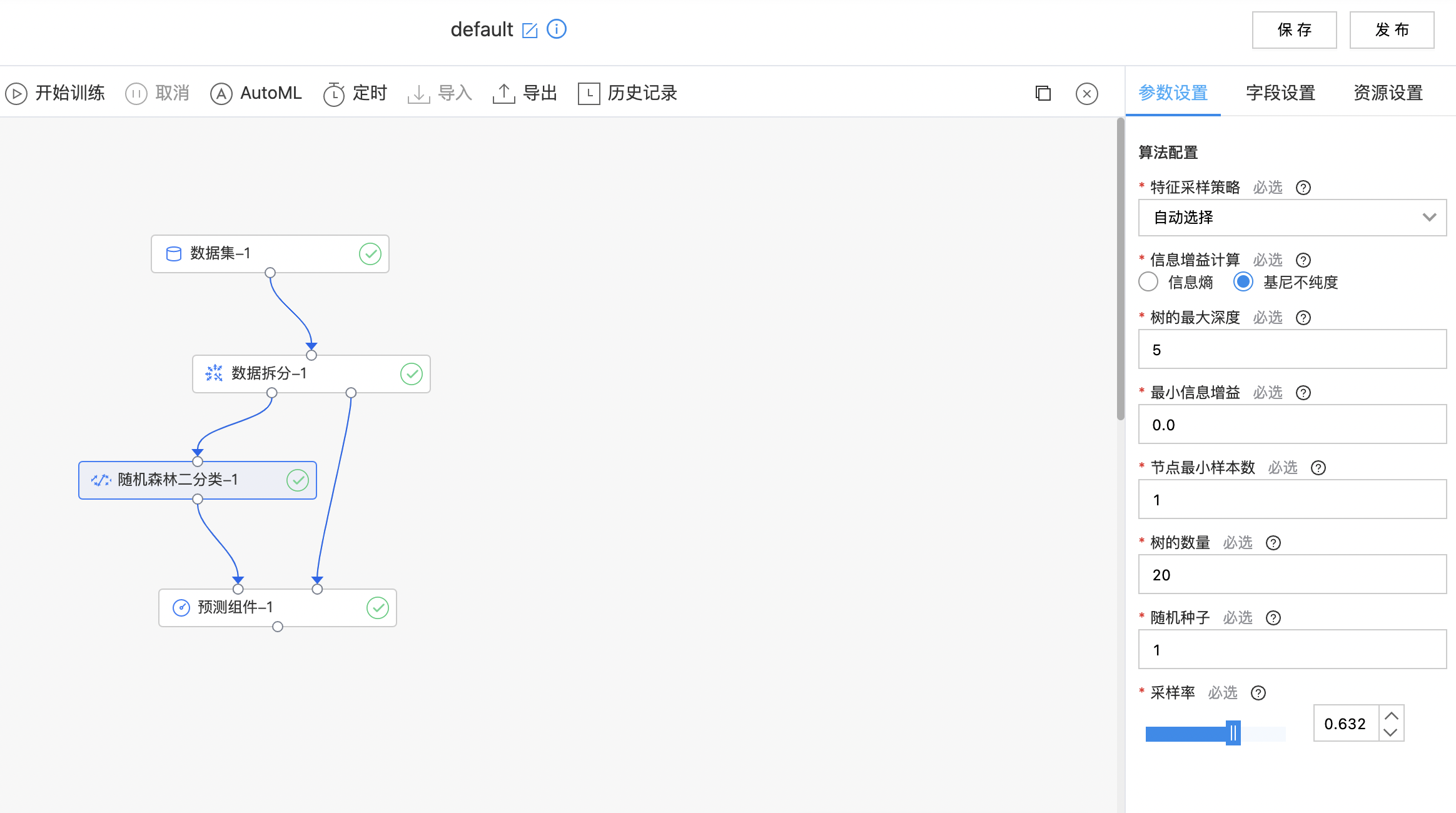
使用示例
构建算子结构,配置参数,完成训练。
随机森林多分类
随机森林多分类是基于随机森林且对应于多分类任务的多分类模型。原理与二分类一样,基学习器为 DecisionTree 多分类,结合策略是使用投票法。
输入
- 输入一个数据集,数据集的特征列double/int,标记列是String或Int类型,标记列唯一值>=3。
输出
- 输出随机森林多分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征采样策略 | 是 | 每次分裂子树时,考虑多少个特征,支持以下策略: 所有特征 自动选择 总特证数以二为底的对数 定值 三分之一的特征 总特征数的一定比例 总特征数的平方根 |
自动选择 |
| 特征采样数 | 是 | 每次分裂子树时,考虑多少个特征 范围:[1, inf) | 10 |
| 信息增益计算 | 是 | 分裂时计算子节点信息增益的策略,目前支持:信息熵、基尼不纯度。 | 基尼不纯度 |
| 树的最大深度 | 是 | 树的最大深度,范围:[2, 30] | 5 |
| 最小信息增益 | 是 | 每次分裂所需的最小信息增益 范围:[0.0, inf) | 0.0 |
| 节点最小样本数 | 是 | 节点最小的样本数,范围:[1, inf) | 1 |
| 树的数量 | 是 | 子树的数量,范围:[1, inf) | 20 |
| 随机种子 | 是 | 随机种子 | 1 |
| 采样率 | 是 | 训练每个子树时,使用的样本占总样本的比例。采样率不宜过小,至少应当保证(训练样本数*采样率>1),否则训练出的模型在预测时会报错 Can not normalize the 0-vector. 范围:[0.001, 0.999] | 0.632 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 是 |
| 标签列 | 是 | 每次分裂子树时,考虑多少个特征。 | 是 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 树的最大深度 | 是 | 最大迭代次数,默认迭代100次 范围:[0, inf) | 5 |
| 最小信息增益 | 是 | 每次分裂所需的最小信息增益 范围:[0.0, inf) | 0.0 |
| 节点最小样本数 | 是 | 节点最小的样本数,范围:[1, inf) | 1 |
| 树的数量 | 是 | 子树的数量,范围:[1, inf) | 20 |
| 采样率 | 是 | 训练每个子树时,使用的样本占总样本的比例。采样率不宜过小,至少应当保证(训练样本数*采样率>1),否则训练出的模型在预测时会报错 Can not normalize the 0-vector. 范围:[0.001, 0.999] | 0.632 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
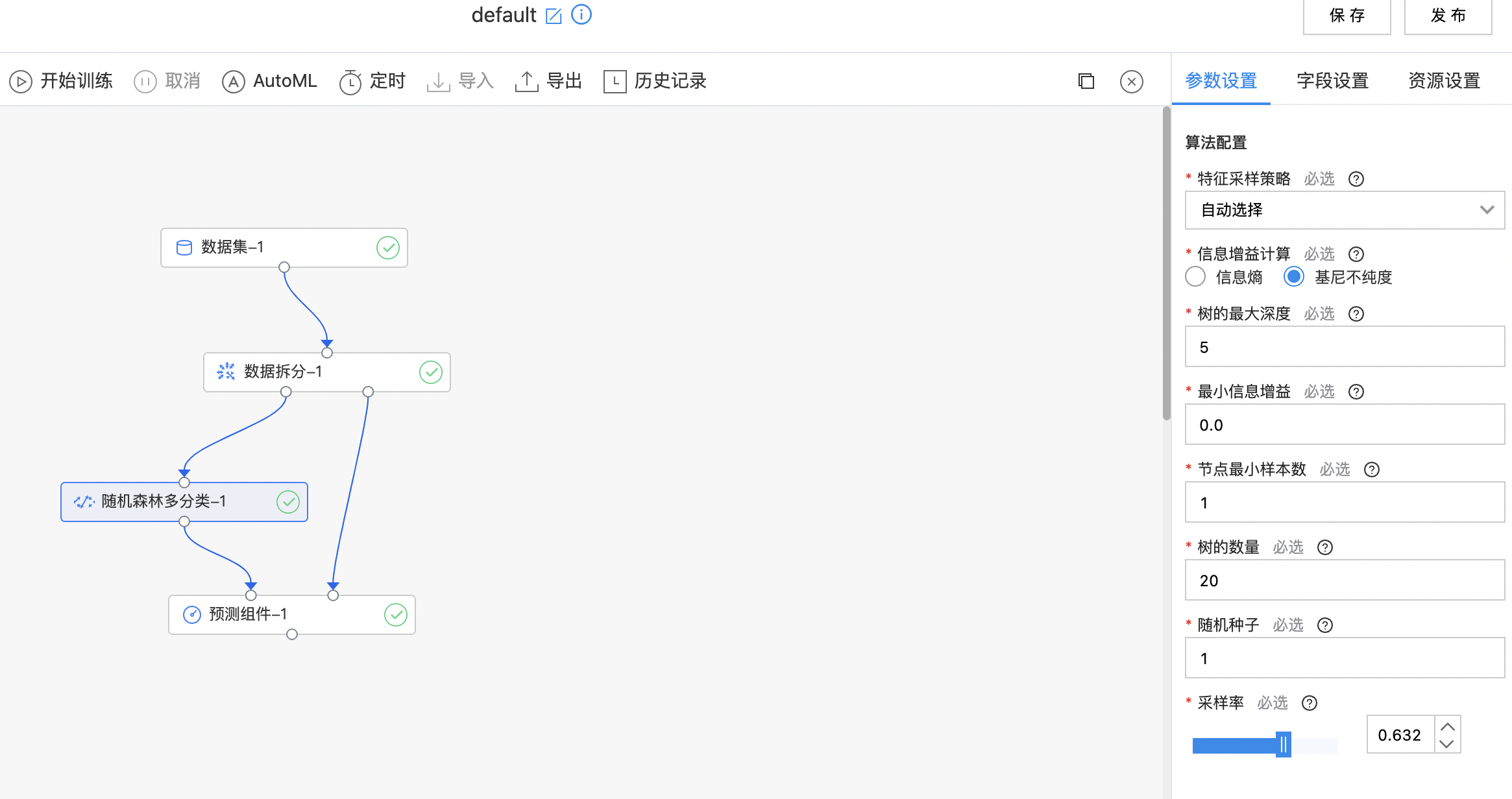
使用示例
构建算子结构,配置参数,完成训练。
GBDT二分类
梯度提升决策树(Gradient Boosting Decision Tree,GBDT)是一种基于boosting集成学习思想的加法模型,训练时采用前向分布算法进行贪婪的学习,每次迭代都学习一棵CART树来拟合之前 t-1 棵树的预测结果与训练样本真实值的残差。
输入
- 输入一个数据集,数据集的特征列必须是数值或数值数组类型,标记列必须是String或Int类型(如果列中的unique值超过了两种,运行算子时会报错)。
输出
- 输出GBDT二分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 树的最大深度 | 是 | GBDT中树(基学习器)的最大深度 范围:[0, inf) | 5 |
| 连续特征分箱数 | 是 | 连续特征的最大分箱数 范围:[2, inf) | 32 |
| 节点最小样本数 | 是 | GBDT中树(基学习器)的节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf) | 1 |
| 最小信息增益 | 是 | GBDT中树(基学习器)分裂时最小信息增益 范围:[0.0, inf) | 0 |
| 训练基学习器选取训练数据集的百分比 | 是 | 每次迭代训练基学习器时所使用的训练数据集的百分比 范围:[1.0E-15, 1.0] | 1 |
| 学习率 | 是 | 学习率,用于缩小(shrinking)每个基学习器的贡献 范围:[1.0E-15, 1.0] | 0.1 |
| 最大迭代轮数 | 是 | 当迭代次数大于该数值时,停止迭代 范围:[1, 200] | 100 |
| 随机种子 | 否 | 随机种子 | 5 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 真实标签列。要求不是数组类型,唯一值是2。 | 无 |
| 正样本标签值 | 否 | 二分类的正样本的标签值,应在标签列中存在 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 树的最大深度 | 是 | GBDT中树(基学习器)的最大深度 范围:[0, inf) | 5 |
| 连续特征分箱数 | 是 | 连续特征的最大分箱数 范围:[2, inf) | 32 |
| 节点最小样本数 | 是 | GBDT中树(基学习器)的节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf) | 1 |
| 最小信息增益 | 是 | GBDT中树(基学习器)分裂时最小信息增益 范围:[0.0, inf) | 0 |
| 训练基学习器选取训练数据集的百分比 | 是 | 每次迭代训练基学习器时所使用的训练数据集的百分比 范围:[1.0E-15, 1.0] | 1 |
| 最大迭代轮数 | 是 | 当迭代次数大于该数值时,停止迭代 范围:[1, 200] | 100 |
| 学习率 | 是 | 学习率,用于缩小(shrinking)每个基学习器的贡献 范围:[1.0E-15, 1.0] | 0.1 |
| 评估标准 | 是 | 选择评估标准: 准确率 pr曲线下面积 roc曲线下面积 F1分数 精确率 召回率 |
roc曲线下面积 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
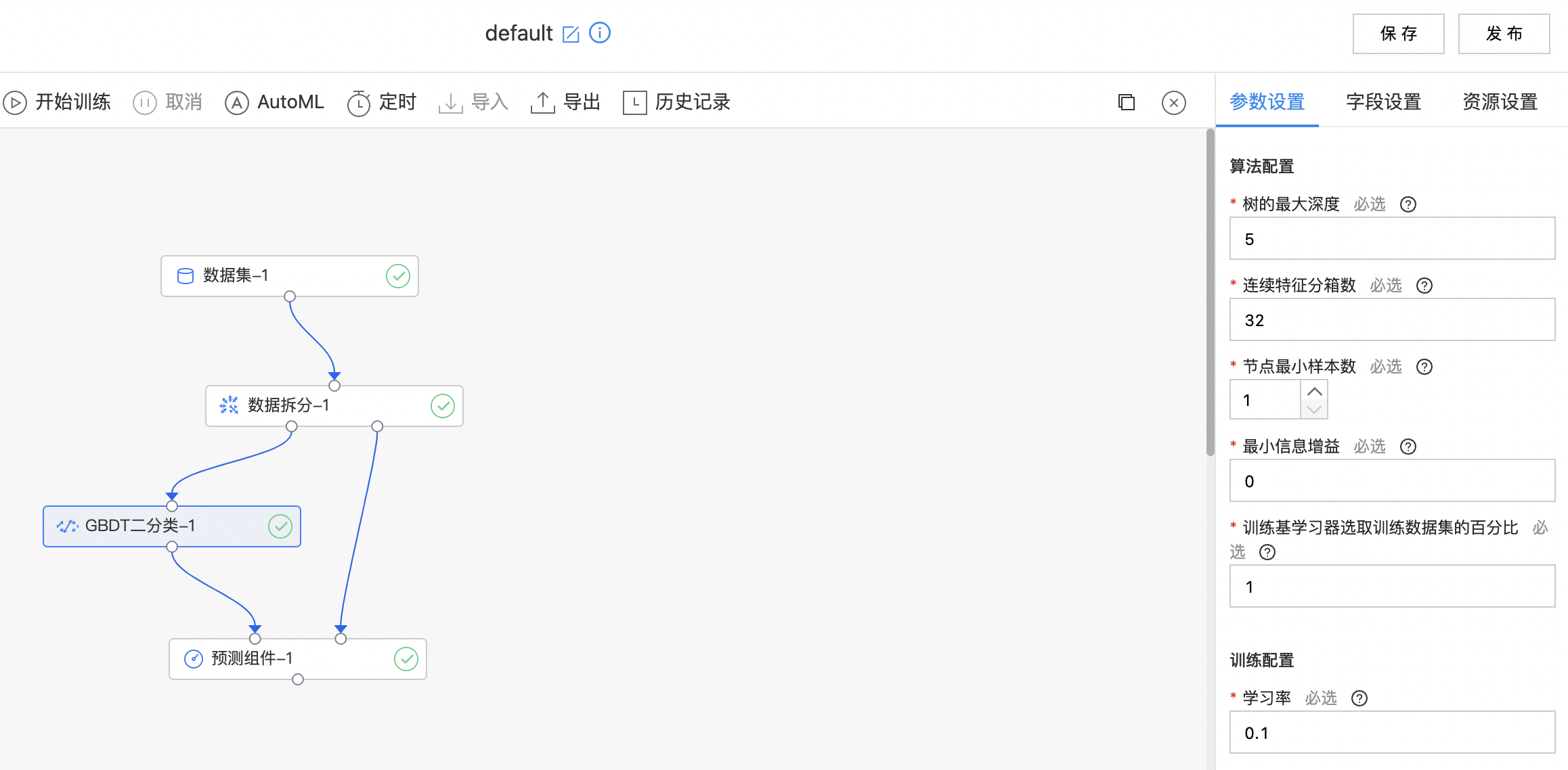
使用示例
构建算子结构,配置参数,完成训练。
GBDT多分类
梯度提升决策树(Gradient Boosting Decision Tree,GBDT)是一种基于boosting集成学习思想的加法模型,训练时采用前向分布算法进行贪婪的学习,每次迭代都学习一棵CART树来拟合之前 t-1 棵树的预测结果与训练样本真实值的残差,对于多分类问题来说,将所有树的分数相加,经过 softmax 函数转换,得到预测结果(类别)。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int或数值数组,标记列必须是String或Int类型(如果列中的unique值不足三种,运行算子时会报错)。
输出
- 输出GBDT多分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 树的最大深度 | 是 | GBDT中树(基学习器)的最大深度 范围:[0, inf)。 | 5 |
| 连续特征分箱数 | 是 | 续特征的最大分箱数 范围:[2, inf) | 32 |
| 节点最小样本数 | 是 | GBDT中树(基学习器)的节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf) | 1 |
| 最小信息增益 | 是 | GBDT中树(基学习器)分裂时最小信息增益 范围:[0.0, inf) | 0 |
| 训练基学习器选取训练数据集的百分比 | 是 | 每次迭代训练基学习器时所使用的训练数据集的百分比 范围:[1.0E-15, 1.0] | 1 |
| 学习率 | 是 | 学习率,用于缩小(shrinking)每个基学习器的贡献 范围:[1.0E-15, 1.0] | 0.1 |
| 最大迭代轮数 | 是 | 当迭代次数大于该数值时,停止迭代 范围:[1, 200] | 100 |
| 随机种子 | 否 | 随机种子 | 5 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求不是数组类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 树的最大深度 | 是 | GBDT中树(基学习器)的最大深度 范围:[0, inf) | 5 |
| 连续特征分箱数 | 是 | 连续特征的最大分箱数 范围:[2, inf) | 32 |
| 节点最小样本数 | 是 | GBDT中树(基学习器)的节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf) | 1 |
| 最小信息增益 | 是 | GBDT中树(基学习器)分裂时最小信息增益 范围:[0.0, inf) | 0 |
| 训练基学习器选取训练数据集的百分比 | 是 | 每次迭代训练基学习器时所使用的训练数据集的百分比 范围:[1.0E-15, 1.0] | 1 |
| 最大迭代轮数 | 是 | 当迭代次数大于该数值时,停止迭代 范围:[1, 200] | 100 |
| 学习率 | 是 | 学习率,用于缩小(shrinking)每个基学习器的贡献 范围:[1.0E-15, 1.0] | 0.1 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
使用示例
构建算子结构,配置参数,完成训练。
SVM二分类
支持向量机(SVM)是基于统计学习理论的一种机器学习方法,通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。 SVM 二分类是线性支持向量机,不是采用核函数方式实现的。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int,标记列必须是String或Int类型(如果列中的unique值超过了两种,运行算子时会报错)。
输出
- 输出SVM二分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 最大迭代次数 | 是 | 控制算法的迭代次数 范围:[1, 10000] | 100 |
| 正则参数 | 是 | 正则参数越大模型越平滑,不容易过拟合 范围:[0.0, inf) | 0.0 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列。要求必须是数值或数值数组类型 | 无 |
| 标签列 | 是 | 真实标签列。要求不是数组类型,唯一值是2。 | 无 |
| 正样本标签值 | 否 | 二分类的正样本的标签值,应在标签列中存在。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 正则参数 | 是 | 正则参数越大模型越平滑,不容易过拟合 范围:[0.0, inf) | 0.0 |
| 最大迭代次数 | 是 | 控制算法的迭代次数 范围:[1, 10000] | 100 |
| 评估标准 | 是 | 选择评估标准: 准确率 F1分数 精确率 召回率 |
F1分数 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
使用示例
构建算子结构,配置参数,完成训练。
SVM多分类
支持向量机(SVM)多分类是基于线性支持向量机(二分类)以及“一对其余”拆分策略得到的多分类模型。
输入
- 输入一个数据集,数据集的特征列必须是Double或Int,标记列必须是String或Int类型(如果列中的unique值不足三种,运行算子时会报错)。
输出
- 输出SVM多分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 最大迭代次数 | 是 | 控制算法的迭代次数 范围:[1, 10000] | 100 |
| 正则参数 | 是 | 正则参数越大模型越平滑,不容易过拟合 范围:[0.0, inf) | 0.0 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型 | 无 |
| 标签列 | 是 | 预测目标列,要求不是数组类型。当数据量或标签数量过大时,需增加内存。 | 无 |
AutoML
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 最大迭代次数 | 是 | 控制算法的迭代次数 范围:[1, 10000] | 100 |
| 正则参数 | 是 | 正则参数越大模型越平滑,不容易过拟合 范围:[0.0, inf) | 0.0 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
使用示例
构建算子结构,配置参数,完成训练。
LR二分类(稀疏)
经典逻辑回归是一个二分类算法,它通过对数几率函数(logistic function)将线性回归模型产生的预测值转化为一个接近 0 或 1 的值,组件支持稀疏数据格式。
输入
- 输入一个数据集,数据集的特征列必须是数值或数值数组或稀疏向量类型,标记列必须是String或Int类型(如果列中的unique值超过了两种,运行算子时会报错)。
输出
- 输出LR二分类(稀疏)模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 二分类阈值 | 是 | 根据二分类阈值将预测结果映射到分类类别上 范围:[0.0, 1.0] | 0.5 |
| 正则化惩罚参数 | 是 | 设置正则化惩罚参数,值越大对模型训练集的拟合系数的惩罚程度越大 范围:[0.0, inf) | 0 |
| ElasticNet参数 | 是 | 正则项的选择,当值为0代表L2正则,当值为1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0] | 0.00 |
| 带截距的回归 | 是 | 是否带截距的回归 | 开启 |
| 标准化处理 | 是 | 是否在训练前对特征标准化处理 | 开启 |
| 最大迭代轮数 | 否 | 当迭代次数大于该数值时,停止迭代 范围:[1, inf) | 100 |
| 目标收敛阈值 | 否 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是稀疏向量类型。 | 无 |
| 标签列 | 是 | 真实标签列。要求不是数组类型,唯一值是2。 | 无 |
AutoML
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 正则化惩罚参数 | 是 | 0 | |
| ElasticNet混合参数 | 是 | 正则项的选择,当值为0代表L2正则,当值为1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0] | 0 |
| 最大迭代轮数 | 是 | 当迭代次数大于该数值时,停止迭代 范围:[1, inf) | 100 |
| 目标收敛阈值 | 是 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
| 评估标准 | 是 | 选择评估标准: 准确率 pr曲线下面积 roc曲线下面积 F1分数 精确率 召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
使用示例
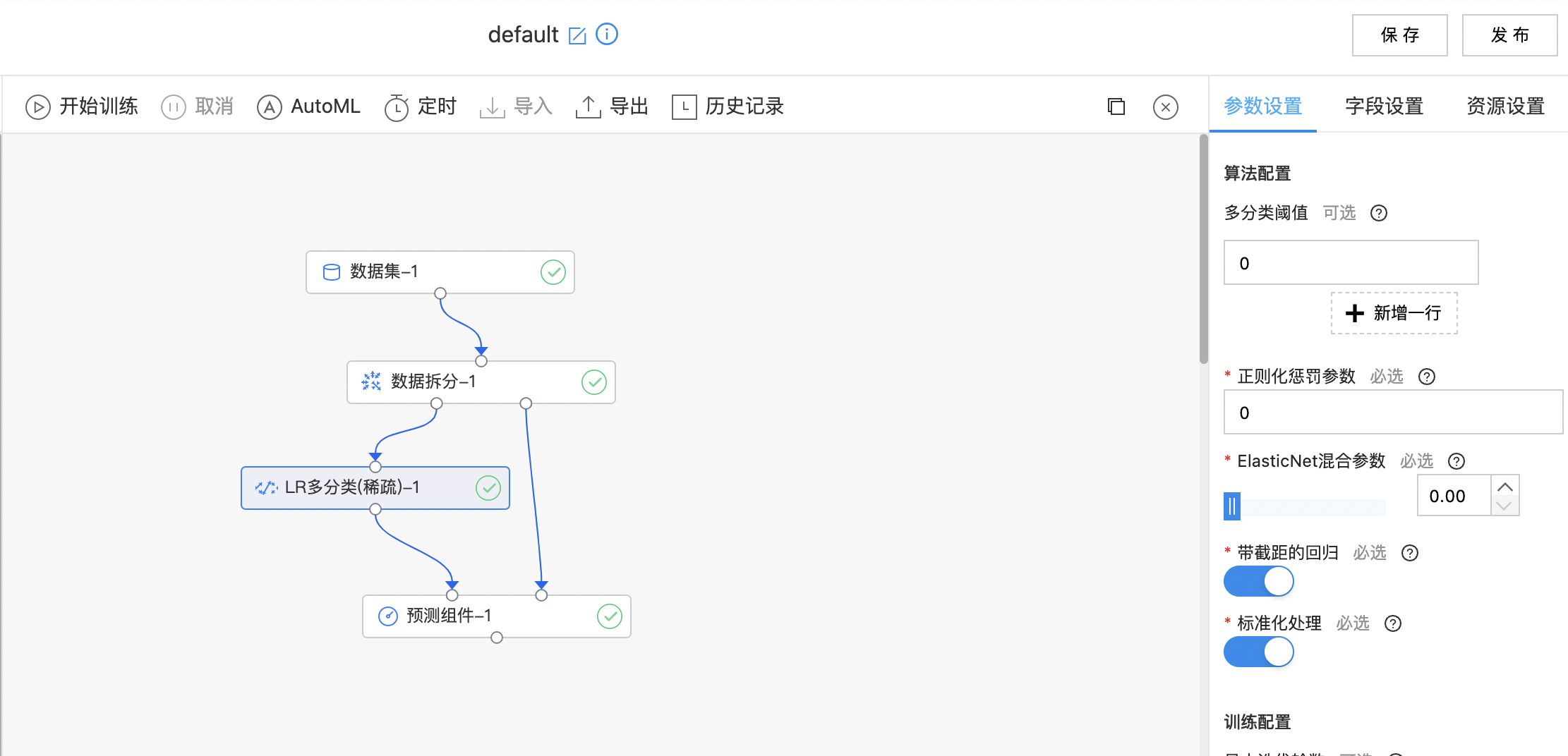
构建算子结构,配置参数,完成训练。
LR多分类(稀疏)
经典逻辑回归的推广,是一个多分类算法。它通过 softmax 函数将线性回归模型产生的预测值转化为多个接近 0 或 1 的值,组件支持稀疏数据格式。
输入
- 输入一个数据集,数据集的特征列必须是数值或数值数组或稀疏向量类型,标记列必须是String或Int类型(如果列中的unique值少于两种,运行算子时会报错)。
输出
- 输出LR多分类(稀疏)模型,支持查看Top10分类的概率。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 多分类阈值 | 是 | 根据多分类阈值以调整预测每个类别的概率,新概率为p/t(其中p为原始概率t是对应类别的阈值),用":"间隔类别标签值和阈值,如labelItem(类别标签值):threshold(类别对应的阈值),每个类别一行,阈值应大于等于0且最多只能有一个0 | 0 |
| 正则化惩罚参数 | 是 | 设置正则化惩罚参数,值越大对模型训练集的拟合系数的惩罚程度越大 范围:[0.0, inf) | 0 |
| ElasticNet参数 | 是 | 正则项的选择,当值为0代表L2正则,当值为1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0] | 0.00 |
| 带截距的回归 | 是 | 是否带截距的回归 | 开启 |
| 标准化处理 | 是 | 是否在训练前对特征标准化处理 | 开启 |
| 最大迭代轮数 | 否 | 当迭代次数大于该数值时,停止迭代 范围:[1, inf) | 100 |
| 目标收敛阈值 | 否 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是稀疏向量类型。 | 无 |
| 标签列 | 是 | 真实标签列,要求不是数组类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 正则化惩罚参数 | 是 | 设置正则化惩罚参数,值越大对模型训练集的拟合系数的惩罚程度越大 范围:[0.0, inf) | 0 |
| ElasticNet混合参数 | 是 | 正则项的选择,当值为0代表L2正则,当值为1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0] | 0 |
| 最大迭代轮数 | 是 | 当迭代次数大于该数值时,停止迭代 范围:[1, inf) | 100 |
| 目标收敛阈值 | 是 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
准确率 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
使用示例
构建算子结构,配置参数,完成训练。
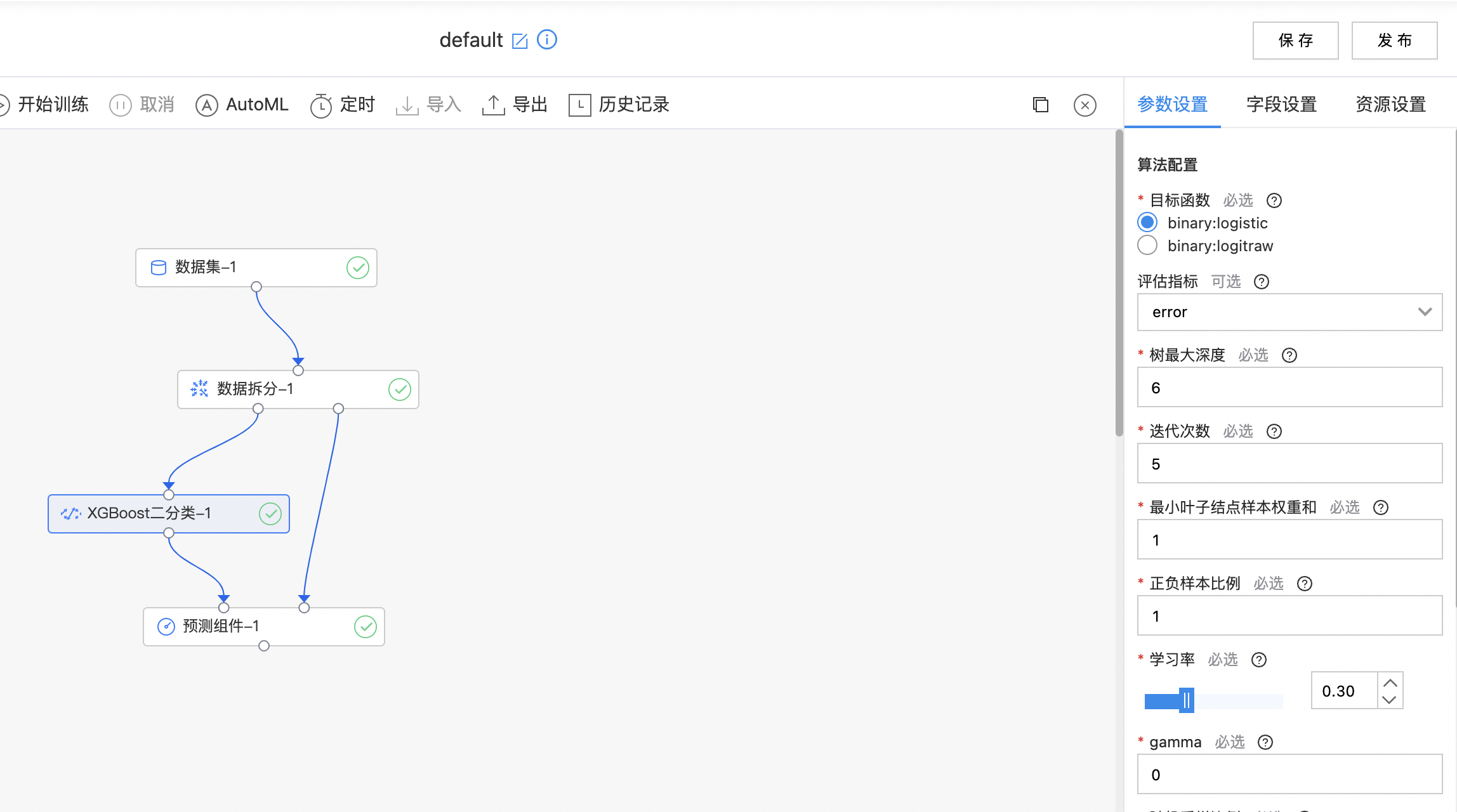
XGBoost二分类
XGBoost是一种提升树模型,它是将多个树模型(CART)集成在一起,形成一个很强的分类器。 对于一个样本,每棵树都会预测出一个结果(分数),对于二分类问题来说,将所有树的分数相加,经过 sigmoid 函数转换,得到预测结果(类别)。
输入
- 输入一个数据集,选择特征列与标签列,特征列要求必须是数值或数值列表类型,标签列要求不是数组类型。
输出
- 输出XGBoost二分类模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 目标函数 | 是 | 待优化的目标函数: binary:logistic binary:logitraw |
binary:logistic |
| 评估指标 | 否 | 评价指标:auc aucpr error logloss |
error |
| 树最大深度 | 是 | xgboost中每棵树的最大深度,树越深通常模型越复杂,更容易过拟合。 范围:[1, inf) | 6 |
| 迭代次数 | 是 | xgboost迭代次数 范围:[1, 200] | 5 |
| 最小叶子节点样本权重和 | 是 | 叶子结点需要的最小样本权重和 范围:[0.0, inf) | 1 |
| 正负样本比例 | 是 | 正负样本比例 范围:[1.0E-8, inf) | 1 |
| 学习率 | 是 | 学习率 范围:[0.0, 1.0] | 0.3 |
| gama | 是 | 节点分裂所需的最小损失函数下降值 范围:[0.0, inf) | 0 |
| 随机采样比例 | 是 | 构造每棵树的所用样本比例(样本采样比例) 范围:[0.01, 1.0] | 1.00 |
| 随机采样特征比例 | 是 | 构造每棵树的所用特征比例 范围:[0.01, 1.0] | 1.00 |
| L1正则化系数 | 是 | L1正则化系数 范围:[0.0, inf) | 0 |
| L2正则化系数 | 是 | L2正则化系数 范围:[0.0, 2.0] | 1 |
| 随机种子 | 是 | 随机种子 | 0 |
| UseExternalMemory | 是 | 是否使用ExternalMemory | 开启 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值列表类型。当数据量过大时,需增加内存。 | 无 |
| 标签列 | 是 | 真实标签列,要求是只有两类的枚举类型。 | 无 |
| 正样本标签值 | 否 | 二分类的正样本的标签值,必须在标签列中存在。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 树最大深度 | 是 | xgboost中每棵树的最大深度,树越深通常模型越复杂,更容易过拟合。 范围:[1, inf) | 6 |
| 迭代次数 | 是 | 迭代次数 | 100 |
| 最小叶子节点样本权重和 | 是 | 叶子结点需要的最小样本权重和 范围:[0.0, inf) | 1 |
| 学习率 | 是 | 学习率 范围:[0.0, 1.0] | 0.3 |
| gamma | 是 | 节点分裂所需的最小损失函数下降值 范围:[0.0, inf) | 0 |
| L1正则化系数 | 是 | L1正则化系数 范围:[0.0, inf) | 0 |
| L2正则化系数 | 是 | L2正则化系数 范围:[0.0, 2.0] | 1 |
| 评估标准 | 是 | 选择评估标准: 准确率 pr曲线下面积 roc曲线下面积 F1分数 精确率 召回率 |
roc曲线下面积 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
使用示例
构建算子结构,配置参数,完成训练,算子支持查看全量特征重要性。
XGBoost多分类
XGBoost 是一种提升树模型,它是将多个树模型(CART)集成在一起,形成一个很强的分类器。 对于一个样本,每棵树都会预测出一个结果(分数),对于多分类问题来说,将所有树的分数相加,经过 softmax 函数转换,得到预测结果(类别)。
输入
- 输入一个数据集,选择特征列与标签列,特征列要求必须是数值或数值列表类型,标签列要求不是数组类型。
输出
- 输出XGBoost多分类模型,支持查看Top10分类的概率。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 评估指标 | 否 | 评价指标: merror mlogloss |
merror |
| 树最大深度 | 是 | xgboost中每棵树的最大深度,树越深通常模型越复杂,更容易过拟合。 范围:[1, inf) | 6 |
| 迭代次数 | 是 | xgboost迭代次数 范围:[1, 200] | 5 |
| 最小叶子节点样本权重和 | 是 | 叶子结点需要的最小样本权重和 范围:[0.0, inf) | 1 |
| 正负样本比例 | 是 | 正负样本比例 范围:[1.0E-8, inf) | 1 |
| 学习率 | 是 | 学习率 范围:[0.0, 1.0] | 0.3 |
| gama | 是 | 节点分裂所需的最小损失函数下降值 范围:[0.0, inf) | 0 |
| 随机采样比例 | 是 | 构造每棵树的所用样本比例(样本采样比例) 范围:[0.01, 1.0] | 1.00 |
| 随机采样特征比例 | 是 | 构造每棵树的所用特征比例 范围:[0.01, 1.0] | 1.00 |
| L1正则化系数 | 是 | L1正则化系数 范围:[0.0, inf) | 0 |
| L2正则化系数 | 是 | L2正则化系数 范围:[0.0, 2.0] | 1 |
| 随机种子 | 是 | 随机种子 | 0 |
| UseExternalMemory | 是 | 是否使用ExternalMemory | 开启 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求不是数组类型。当数据量或标签数量过大时,需增加内存。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9] | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10] | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10] | 5 |
| 树最大深度 | 是 | xgboost中每棵树的最大深度,树越深通常模型越复杂,更容易过拟合。 范围:[1, inf) | 6 |
| 迭代次数 | 是 | 迭代次数 | 100 |
| 最小叶子节点样本权重和 | 是 | 叶子结点需要的最小样本权重和 范围:[0.0, inf) | 1 |
| 学习率 | 是 | 学习率 范围:[0.0, 1.0] | 0.3 |
| gamma | 是 | 节点分裂所需的最小损失函数下降值 范围:[0.0, inf) | 0 |
| L1正则化系数 | 是 | L1正则化系数 范围:[0.0, inf) | 0 |
| L2正则化系数 | 是 | L2正则化系数 范围:[0.0, 2.0] | 1 |
| 评估标准 | 是 | 选择评估标准: 准确率 加权F1分数 加权精确率 加权召回率 |
roc曲线下面积 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
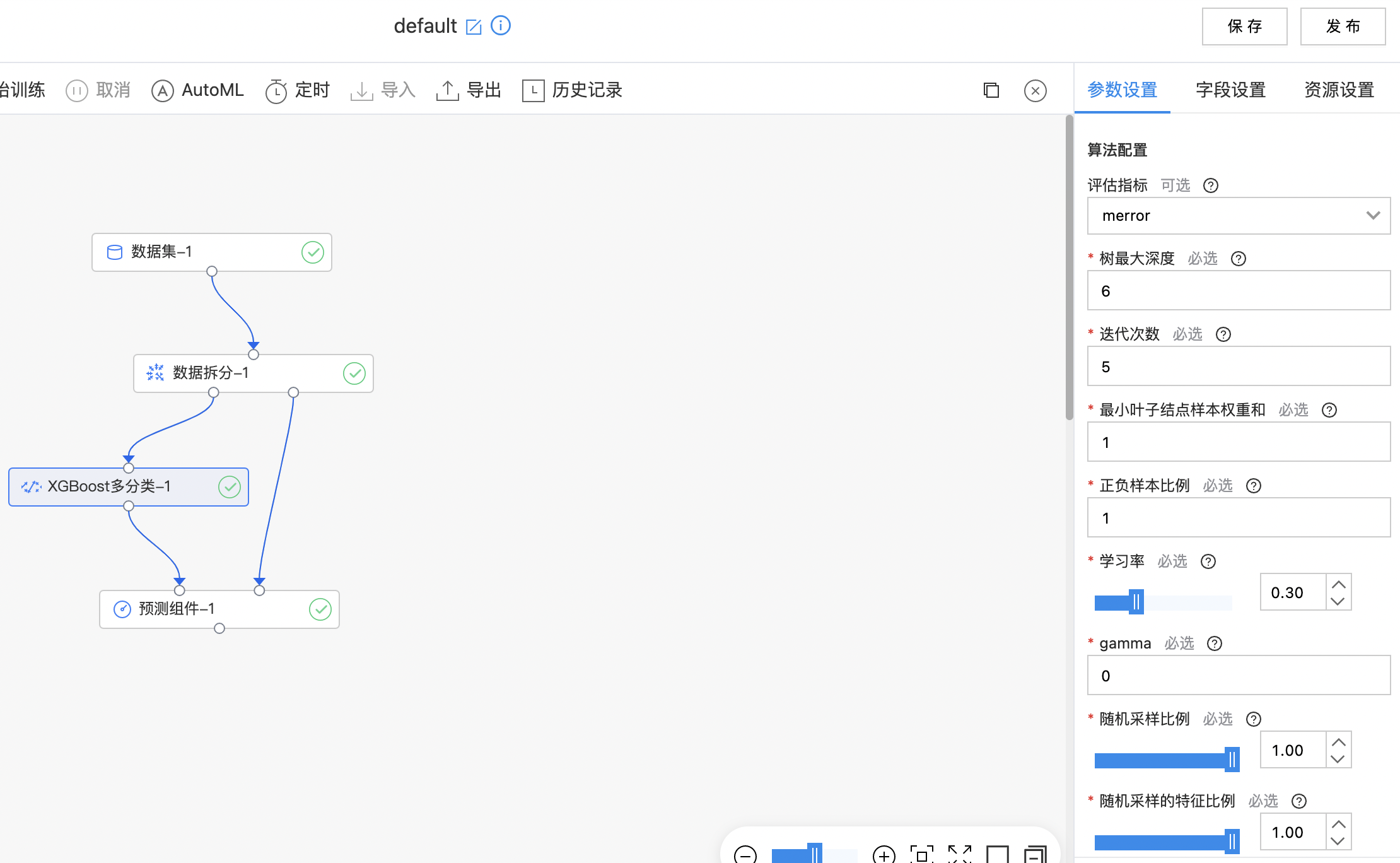
使用示例
构建算子结构,配置参数,完成训练,算子支持查看全量特征重要性。