时间序列组件

ARIMA

ARIMA(Autoregressive Integrated Moving Average)差分自回归移动平均模型，时间序列预测分析方法之一。 ARIMA(p,d,q)中，AR是自回归，p为自回归项数；MA为移动平均，q为移动平均项数，d为使之成为平稳序列所做的差分次数(阶数)。

输入

• 输入一个数据集，需要指定排序列、数值列。
• 排序列为对时间序列进行排序的列（基本为数值列）要求数值非空且有序，数值列为时间序列，根据此列进行时间序列运算，要求非空的数值列。

输出

• 输出一个数据集，该数据集只含有一列(时间序列的预测结果，行数为预测步长。

算子参数

参数名称	是否必选	参数描述	默认值
ARIMA中p值	是	ARIMA中p值，代表AR中的自回归项数，该值必须为正 范围：[0, inf)	1
ARIMA中d值	是	ARIMA中d值，代表差分次数，该值必须为正 范围：[0, 2]	0
ARIMA中q值	是	ARIMA中q值，代表MA中的移动平均项数，该值必须为正 范围：[0, inf)	0
预测的步长	是	基于时间序列预测的未来时间步长 范围：[1, inf)	1

字段参数

参数名称	是否必选	参数描述	默认值
排序列	是	时间序列依据此列由小到大排序，一般选择日期列且不能有重复值	无
数值列	是	时间序列的数值列，步长与结果数据集的行数一致，该列必须为数值	无

计算逻辑

使用示例

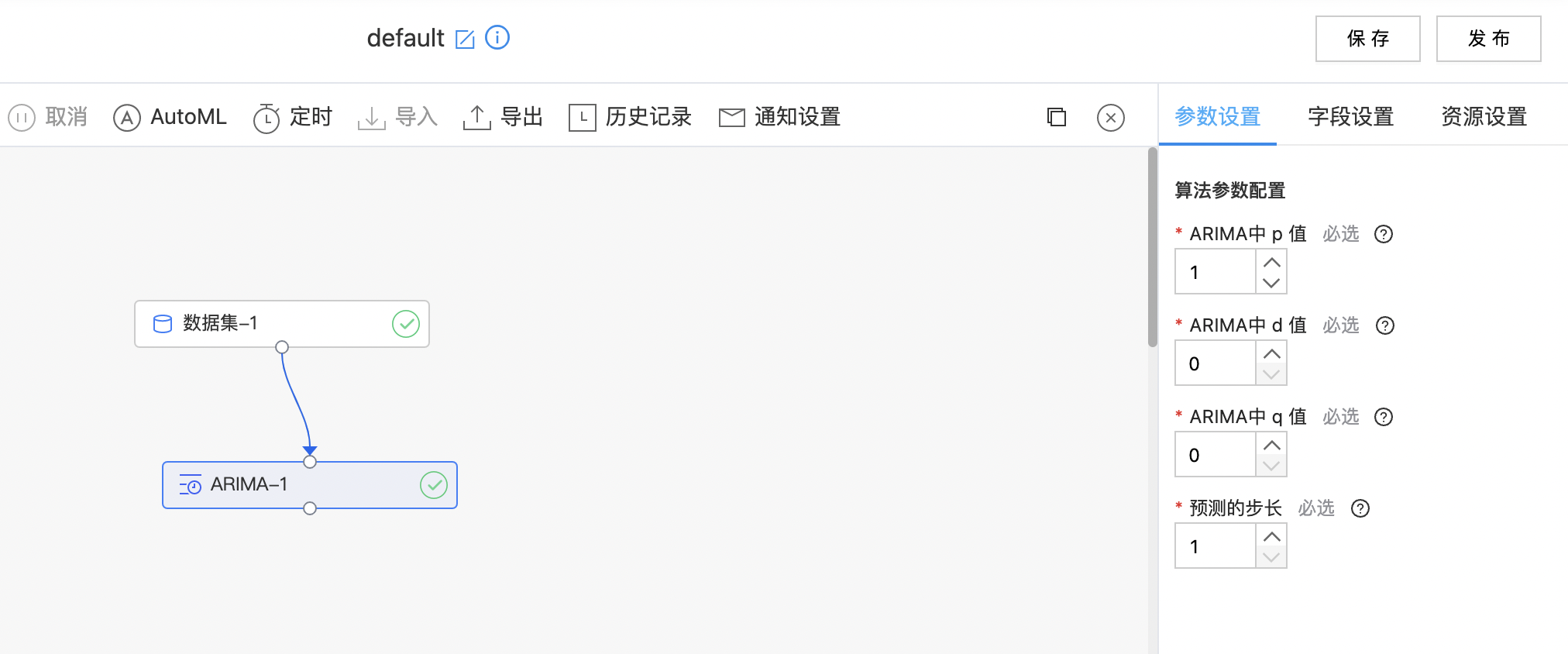
1. 构建算子结构，配置参数，完成训练。

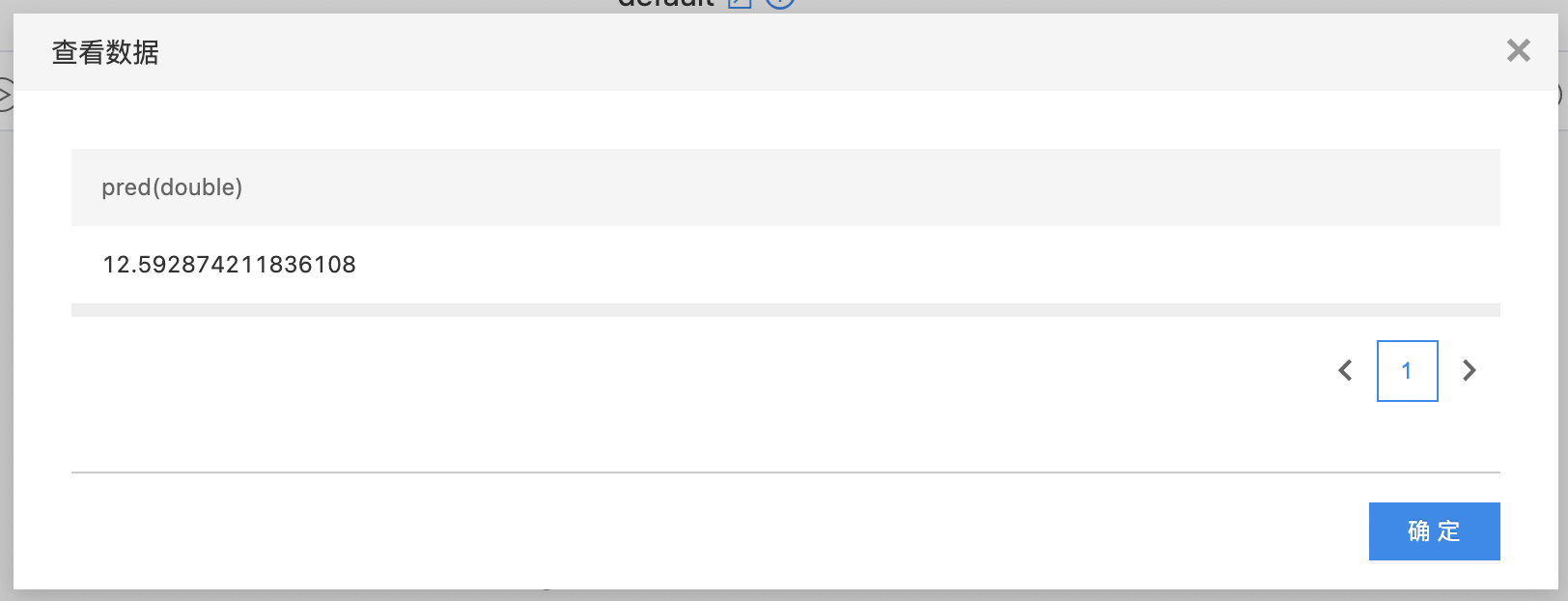
2. 查看训练结果。

AutoARIMA

AutoARIMA差分整合移动平均自回归模型，时间序列预测分析方法之一。AutoARIMA通过超参搜索查询最优的ARIMA模型。 Auto-ARIMA通过进行差异测试来确定差分d，然后在定义的p、q起始值和p、q最大值，的范围内拟合模型。如果启用了季节性可选参数，在确定季节性差分d的最佳顺序之后，还将寻求找出最佳的p、q超参数。

注意：由于平稳性问题，auto-ARIMA可能找不到会收敛的合适模型。如果是这种情况，将抛出ValueError，建议在重新拟合之前采取诱导平稳性的措施，或者选择新的搜索范围。

输入

• 输入一个数据集，包括排序列、数值列。
• 排序列为对时间序列进行排序的列（基本为数值列）要求数值非空且有序；数值列为时间序列列根据此列进行时间序列运算，要求非空的数值列。

输出

• 第一个输出是模型报告，包含搜索出的模型，模型的AIC、BIC、HQIC、Log Likehood。
• 第二个输出是预测结果，行数与预测的步长一致。

算子参数

参数名称	是否必选	参数描述	默认值
是否训练季节性ARIMA	是	是否适合季节性的ARIMA，默认是真。注意，如果季节性为真且频率为1时，季节性将为假。	开启
季节性频率	是	每个季节周期观测的频率。例如，每年观测一次（非季节性数据）则频率为1，每个季度观测一次则频率为4，每个月观测一次则频率为12，每周观测一次则频率为52，每天观测一次则频率为7。 范围：[1, inf)。	1
p、q起始值	是	p为自回归(AR)模型的阶数(或时滞数)。q是MA模型的阶数，起始值必须是一个正整数。 范围：[1, inf)。	2
p、q最大值	是	p、q最大值, 必须是个大于等于p、q起始值的正整数 范围：[1, inf)。	5
差分d	是	一阶微分的阶数，必须为-1或正整数。设置为-1时将根据测试结果自动选择该值。如果为-1，运行时间会相对较长 范围：[-1, inf)。	-1
差分d最大值	是	差分d最大值, 必须是个大于等d的正整数 范围：[1, inf)。	2
季节性p、q起始值	是	季节性模型设置的p、q最大值，必须是个大于等于p、q起始值的正整数。 范围：[1, inf)。	1
季节性p、q最大值	是	季节性模型设置的p、q最大值，必须是一个正整数。 范围：[1, inf)。	2
季节性差分d	是	季节性差分d，必须为-1或正整数。设置为-1时将根据测试结果自动选择该值。如果为-1，运行时间会相对较长 范围：[-1, inf)。	-1
季节性差分d最大值	是	季节性模型设置的差分d最大值，必须是个大于等于季节性差分d的正整数。 范围：[0, inf)。	1
最优化方法	是	搜索模型过程中采用的最优化方法： nm：Nelder-Mead bfgs：Broyden-Fletcher-Goldfarb-Shann lbfgs：有限内存BFGS powell：Powell方法 cg：共轭梯度法	bfgs
显著性	是	测试显著性 范围：[0.0, 1.0]。	0.05
最大迭代次数	是	搜索模型的最大迭代次数 范围：[1, inf)。	50
预测的步长	是	基于时间序列预测的未来时间步长 范围：[1, inf)。	10

字段参数

参数名称	是否必选	参数描述	默认值
排序列	是	时间序列依据此列由小到大排序，一般选择日期列且不能有重复值。	无
数值列	是	时间序列的数值列，该列必须为数值。	无

使用示例

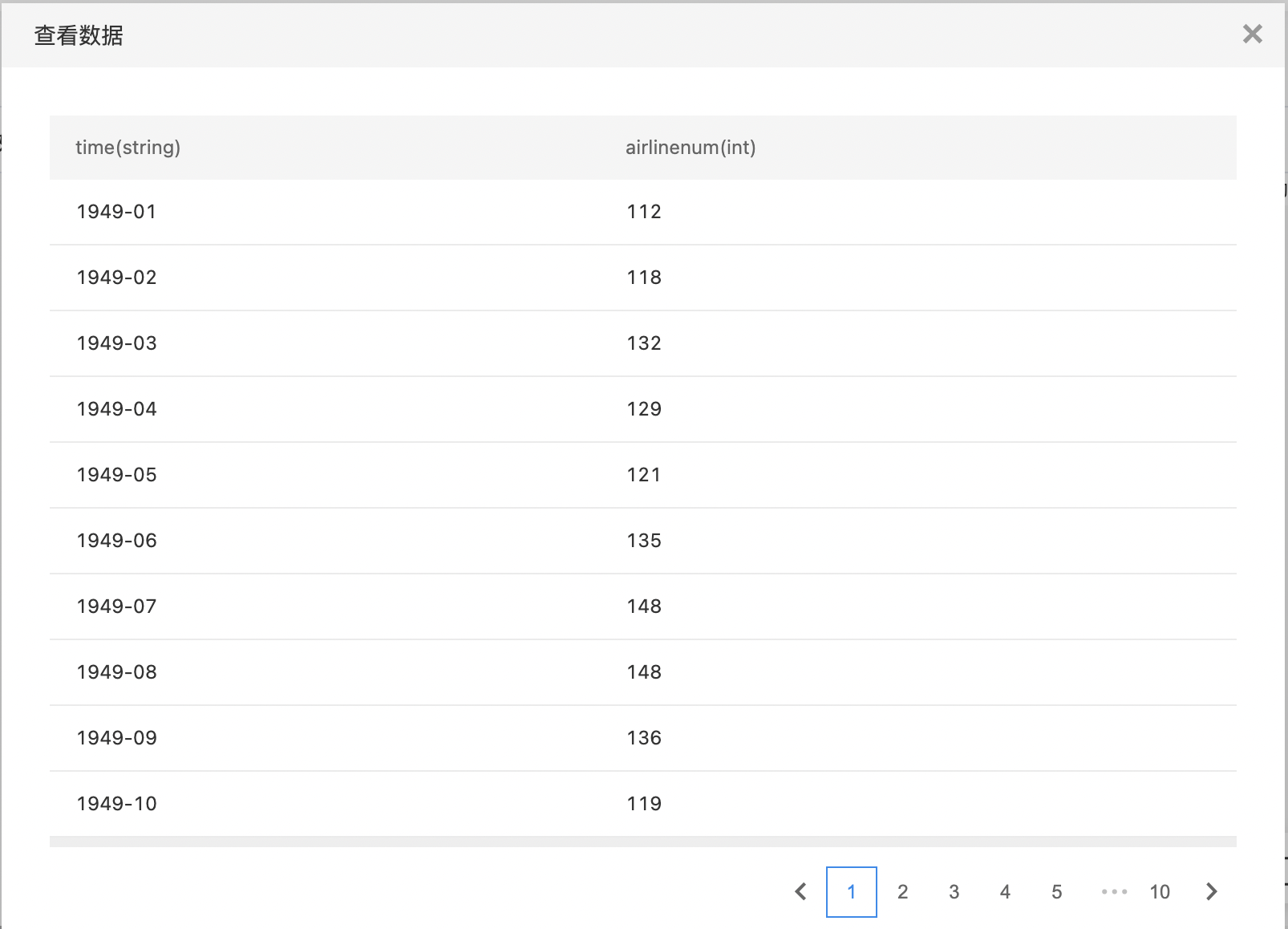
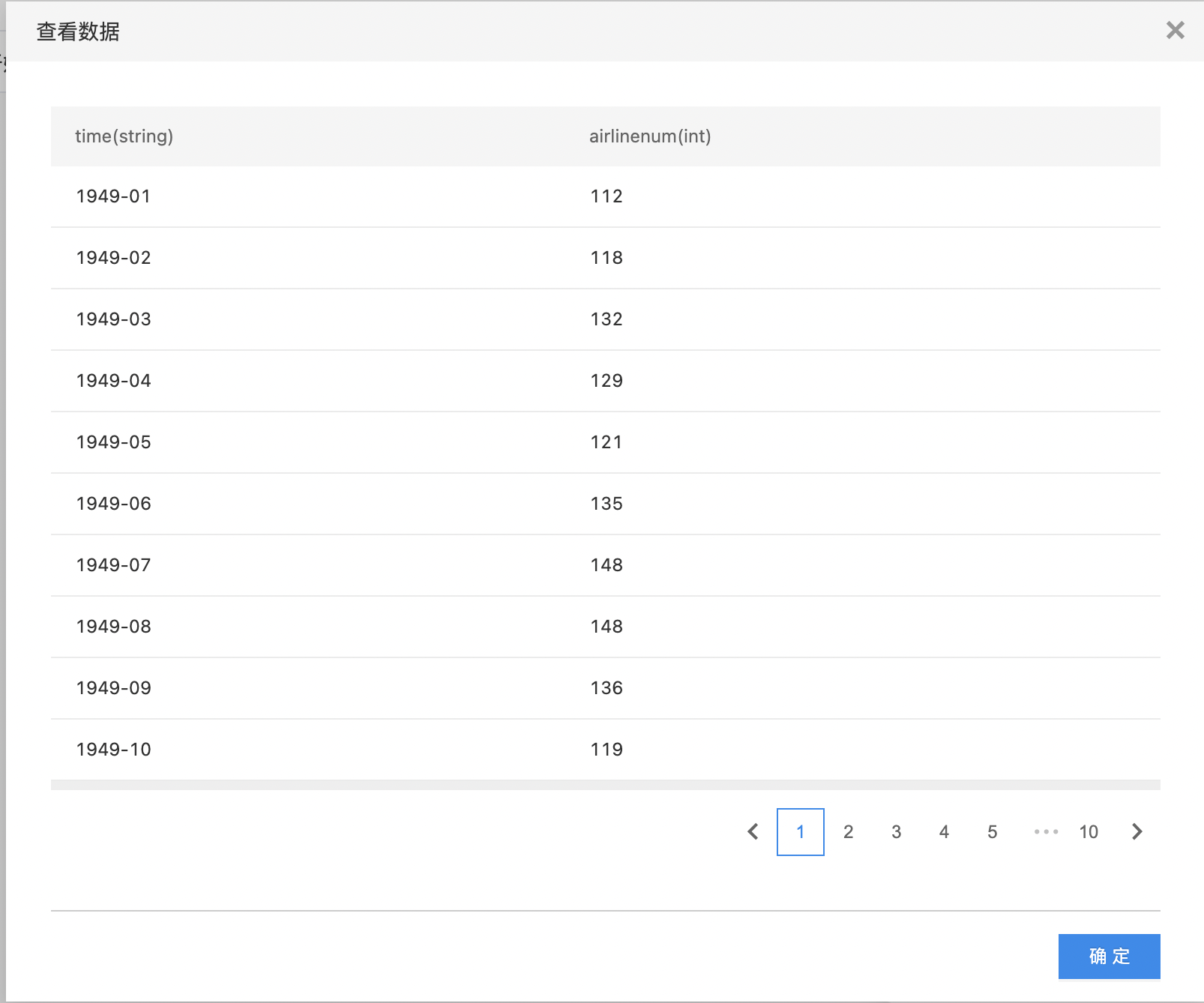
1. 查看原始数据，数据集包含两列：time-时间列、airlinenum-数值列，可以得知航线数量是每天观测一次。

2. 算子连接方式如下，选择默认参数，完成训练。

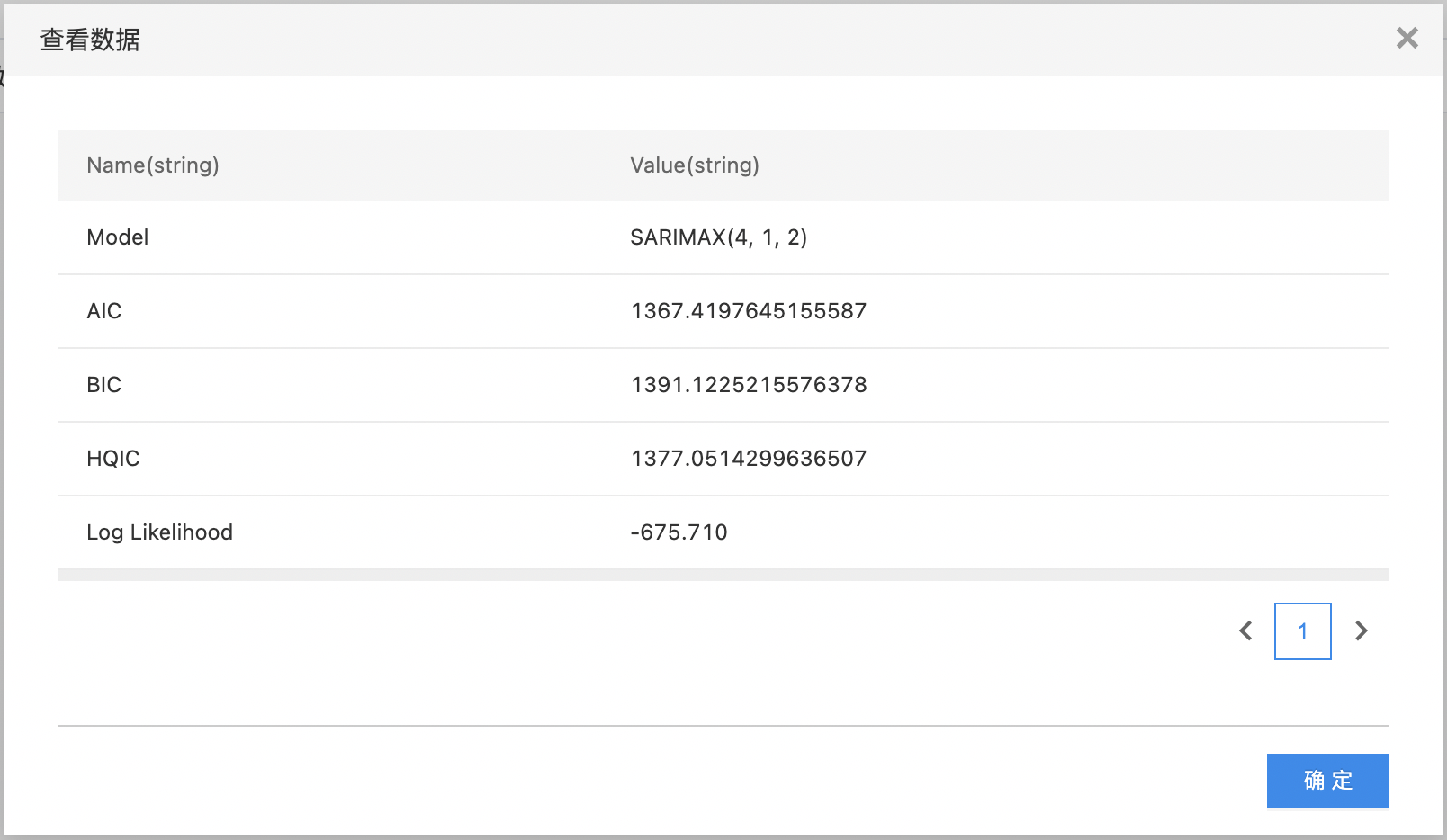
3. 查看模型报告。

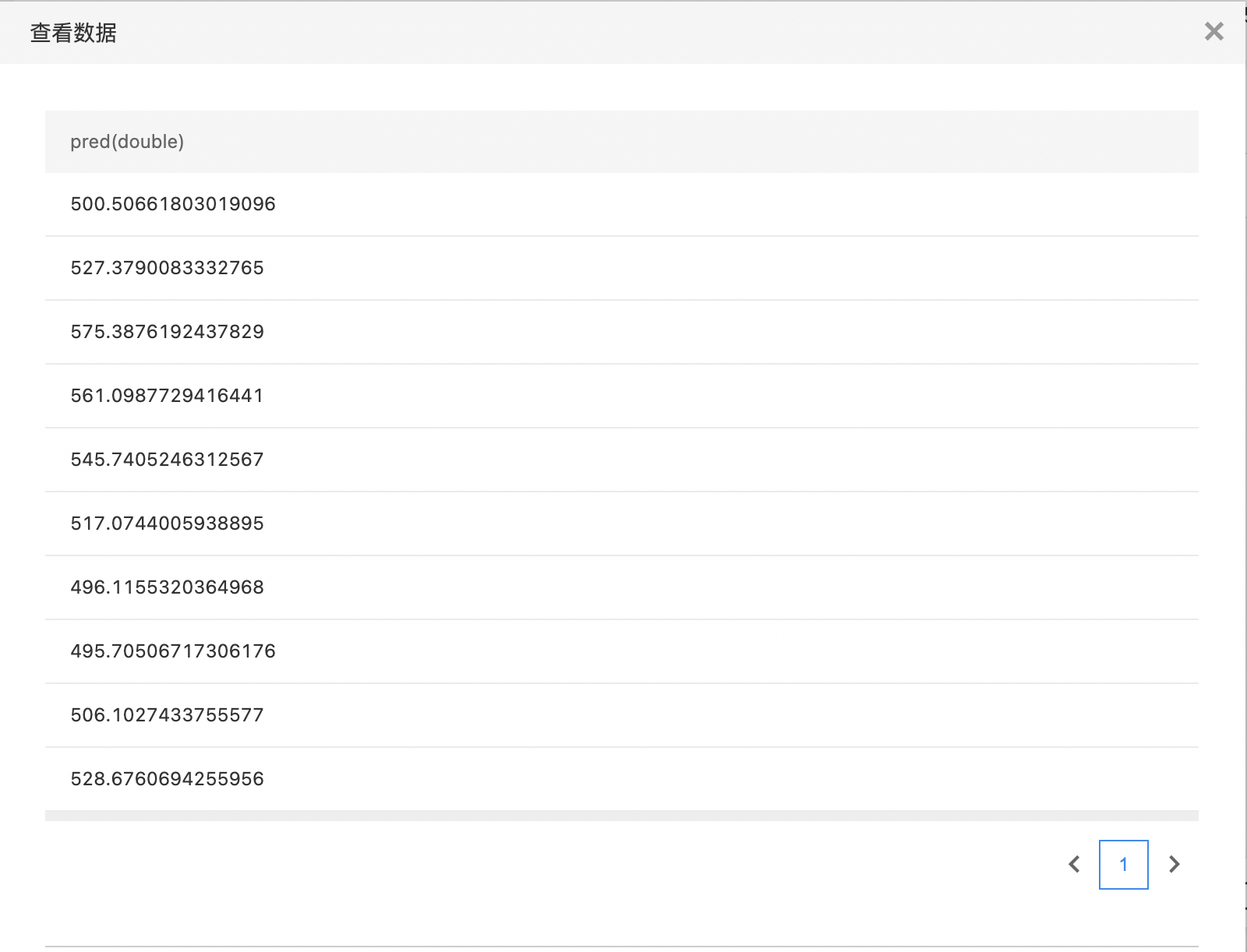
4. 查看预测结果。

AR

AR（auto-regressive）模型是自回归模型，时间序列预测分析方法之一。其原理是利用观测点前若干时刻的变量的线性组合来描述观测点后若干时刻变量的值，属于线性回归模型。

输入

• 输入一个数据集，需要指定排序列、数值列。
• 排序列为对时间序列进行排序的列（基本为数值列）要求数值非空且有序，数值列为时间序列列根据此列进行时间序列运算，要求非空的数值列。

输出

• 输出一个数据集，该数据集只含有一列(时间序列的预测结果)，行数为预测步长。

算子参数

参数名称	是否必选	参数描述	默认值
AR中的p值	是	AR中p值 ，代表自回归项数，范围：[1, inf)。	1
预测的步长	是	基于时间序列预测的未来时间步长，步长与结果数据集的行数一致，范围：[1, inf)。	1

字段参数

参数名称	是否必选	参数描述	默认值
排序列	是	时间序列依据此列由小到大排序，一般选择日期列且不能有重复值	无
数值列	是	时间序列的数值列，该列必须为数值	无

使用示例

构建算子结构，配置参数，完成训练。

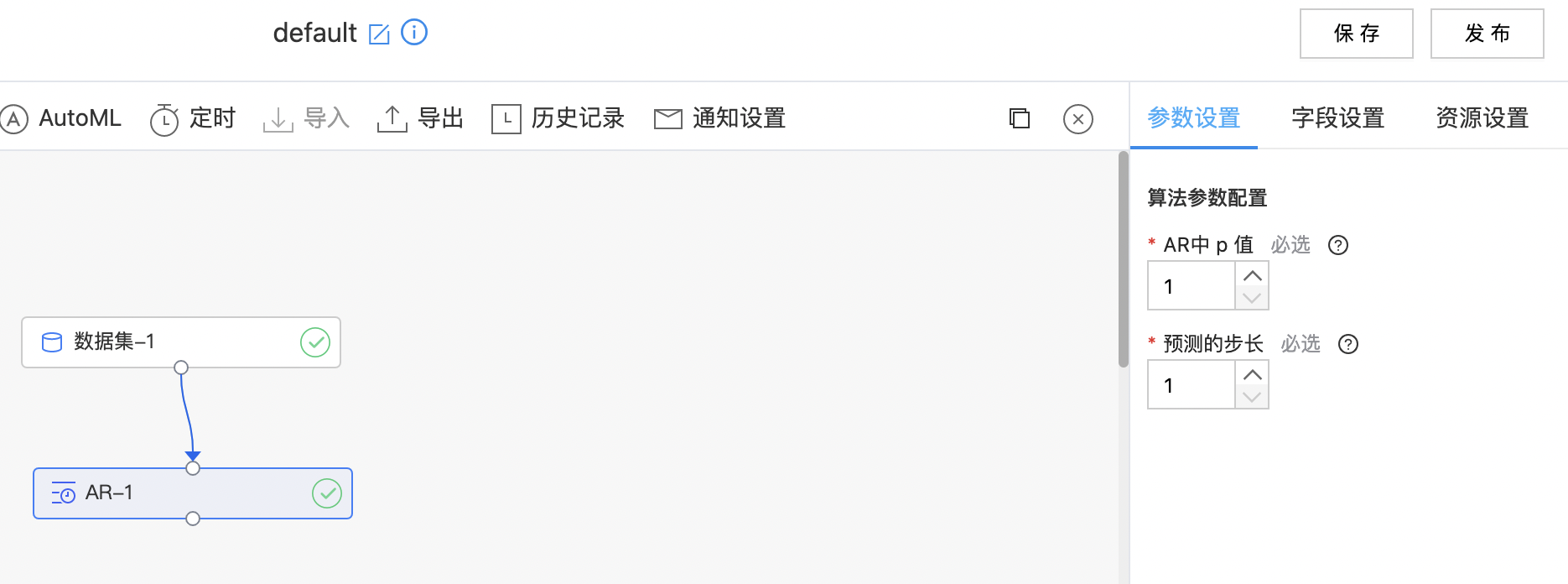
DeepAR

DeepAR 是Amazon提出的基于深度学习的时间序列预测方法。DeepAR 是一种适用于时间序列预测的监督学习算法，该算法使用递归神经网络 (RNN) 生成点预测和概率预测。传统的时间序列预测方法（ARIMA、Holt-Winters’ 等）往往针对一维时间序列本身建模，难以利用额外特征。此外，传统方法的预测目标通常是序列在每个时间步上的取值。与之相比，基于神经网络的 DeepAR 方法可以很方便地将额外的特征纳入考虑，且其预测目标是序列在每个时间步上取值的概率分布。

输入

• 输入一个数据集，需要指定排序列、数值列。排序列为对时间序列进行排序的列要求为符合此列应为日期列且需要满足Timestamp中日期类型。数值列为时间序列列根据此列进行时间序列运算，要求非空的数值列。

输出

• 输出一个数据集，该数据集只含有一列(时间序列的预测结果)，行数为预测步长。

算子参数

参数名称	是否必选	参数描述	默认值
DeepAR中RNN的类型	是	DeepAR中RNN的类型： lstm gru	lstm
DeepAR中的RNN层数	是	DeepAR中RNN层数 范围：[1, inf)	2
DeepAR中RNN的神经元个数	是	DeepAR中RNN的神经单元个数 范围：[10, inf)	40
时间序列中的观测频率	是	时间序列中的观测频率，需要和排序列时间频率一致且为Pandas中频率类型，通常用M、D、H等，例如1M代表1个月，1D代表1天，1H代表1小时。	无
预测的步长	是	基于时间序列预测的未来时间步长 范围：[1, inf)	1
训练学习率	是	训练中的学习率 范围：[1e-06, 1.0]	0.001
训练轮数	是	训练轮数 范围：[1, inf)	100
训练batch的大小	是	训练batch大小 范围：[1, inf)	32
DeepAR中的DropOut	是	DeepAR中的DropOut 范围：[0.0, 1.0]	0.1

字段参数

参数名称	是否必选	参数描述	默认值
排序列	是	时间序列依据此列由小到大排序，此列应为日期列且需要满足Timestamp中日期类型且不能有重复值	无
数值列	是	时间序列的数值列，该列必须为数值	无

使用示例

1. 查看原始数据。

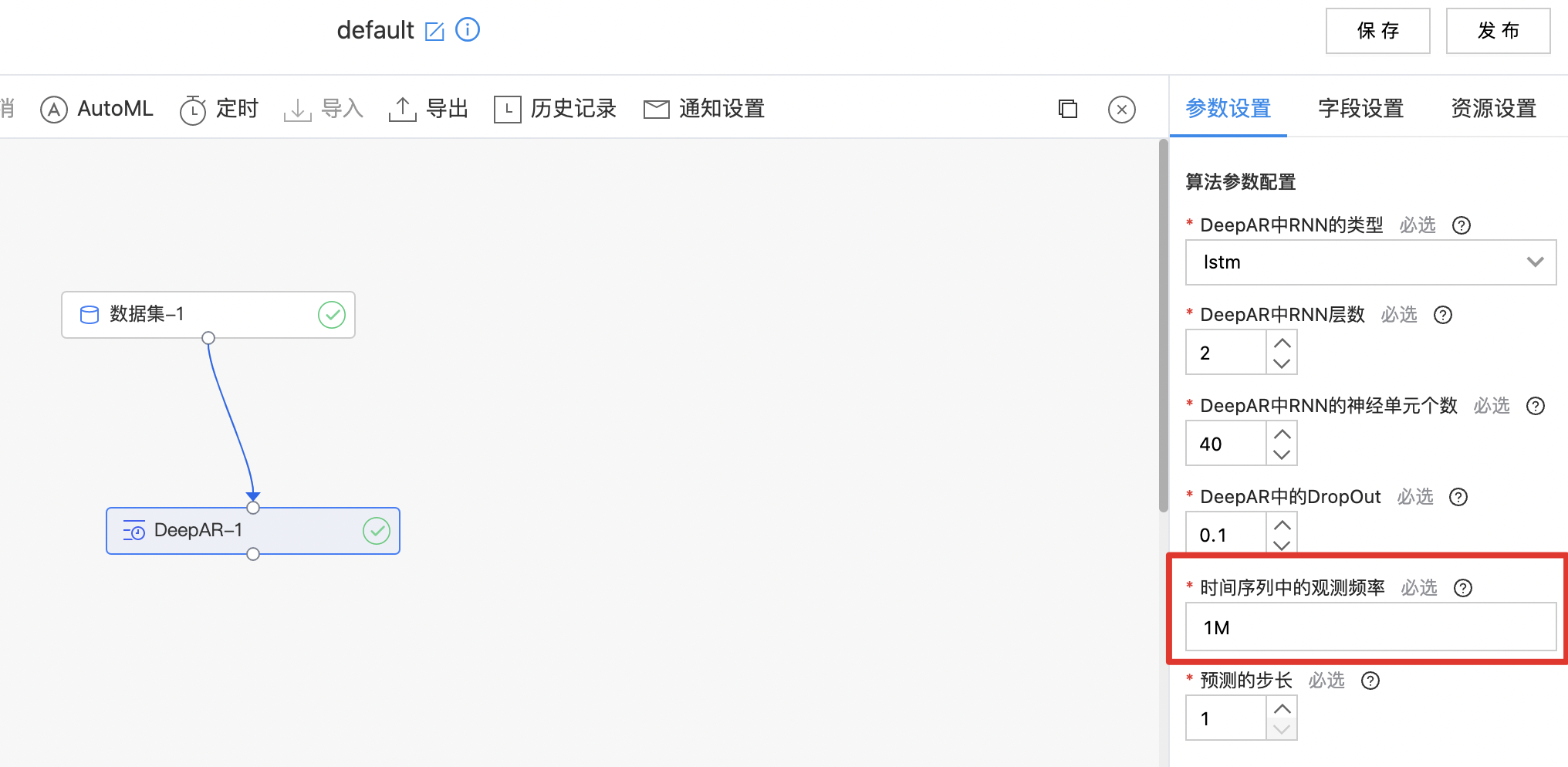
2. 构建算子结构，配置参数，在本示例中，时间序列中的观测频率为"1M"，完成训练。

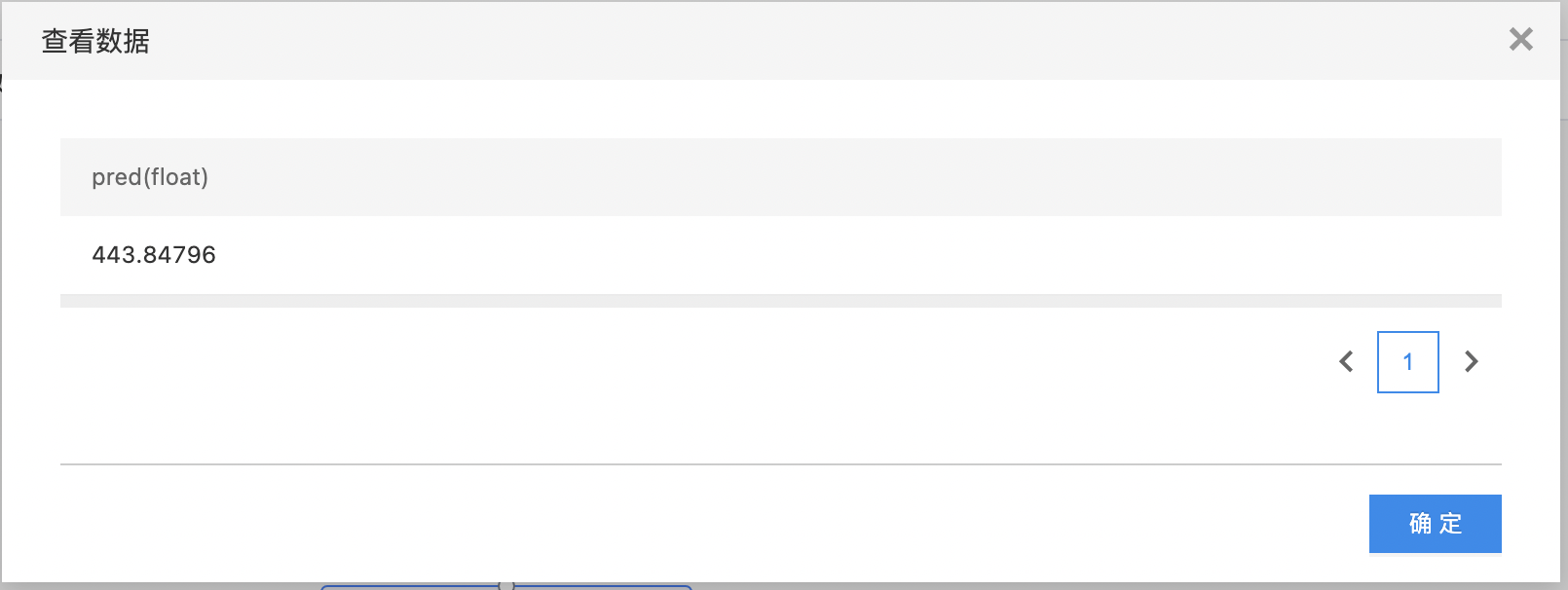
3. 查看输出结果。

Prophet

Prophet是基于非线性趋势与年度、每周和每日季节性以及假日效应的附加模型预测时间序列数据的过程，支持趋势、季节性周期变化及节假日效应。

输入

输入两个数据集，其中训练数据集必选，节假日数据集可选。

输出

输出一个数据集

算子参数

参数名称	是否必选	参数描述	默认值
growth	是	增长趋势项。支持两种增长趋势项模型：linear，logistic。	linear
automatic_changepoint_selection	是	自动变点选择。若选“no", 则表示手动指定变点。	Yes
change point_range	是	变点选择范围。基于时间序列的前指定比例范围的历史数据选择变点， 范围：[0.0, 1.0]。	0.80
n_changepoints	是	变点数。从历史数据前changepoint_range比例中均匀选择的变点个数， 范围：[0, inf)	25
change point_prior_scale	是	变点灵活度。调整自动变点选择的灵活性。较大的值将允许更多的变点，较小的值将允许较少的变点。值越大，模型对历史数据的拟合程度越强。建议取值在0.001和0.5之间， 范围：[1e-15, inf)	0.05
yearly_seasonality	是	适应年季节性。支持三种模式：auto，true，false。	Auto
weekly_seasonality	是	适应周季节性。支持三种模式：auto，true，false。	Auto
daily_seasonality	是	适应日季节性。支持三种模式：auto，true，false。	Auto
seasonality_mode	是	季节性方式。支持两种方式：additive(加法模型），multiplicative（乘法模型）。	additive
seasonality_prior_scale	是	季节性强度。调整季节性模型的强度，较大的值可使模型适应较大的季节性波动，较小的值会抑制季节性。建议取值在0.01和10之间， 范围：[1e-15, inf)。	10.0
holiday_prior_scale	是	节假日强度。调整节假日成分模型的强度，仅输入holidays时有效。建议取值在0.01和10之间， 范围：[1e-15, inf)。	10.0
mcmc_samples	是	MCMC样本。非负整数，如果大于0，将对指定数量的MCMC样本进行完整的贝叶斯推断，如果为0，将进行最大后验概率估计 范围：[0, inf)。	0
Interval_samples	是	区间宽度。为预测提供的不确定性区间的宽度，如果mcmc_samples为0，这将只是使用外推生成模型的最大后验概率估计的趋势中的不确定性；如果mcmc_samples大于0，这将被整合到所有模型参数中，包括季节性的不确定性。 范围：[-1.0, 1.0]	0.80
uncertainty_samples	是	模拟样本。用于估计不确定性区间的模拟抽样次数 范围：[1, inf)。	1000

预测参数配置

参数名称	是否必选	参数描述	默认值
periods	是	向前预测的整数周期数。 范围：[0, inf)。	7
freq	是	日期频率。频率可以有倍数，例如，5H表示5个小时。请输入有效频率。常用频率单位：S(秒)，T(分)，H(时)，D(日历日)，B(工作日)，W(周)，MS(月初)，M(月底)，Q(季度末)，Y(年末)。	D
include_history	是	包括历史日期。将历史日期包括在预测数据中。如果选择不包括历史日期，periods值需要设置为大于0。	no

字段参数

参数名称	是否必选	参数描述	默认值
时间列	是	时间序列。要求是日期类型或日期格式的字符串类型。时间列不可以包含空值。日期格式样例：2021-01-01 00:00:00。	无
预测列	是	时间序列预测列。要求是数值类型。预测列可以包含空值，要求非空值样本不少于2。	无
节假日名称列	否	节假日名称列。要求是字符串类型。输入holidays时有效且必选。节假日名称列不可以包含空值。	无
节假日时间列	否	节假日时间列。要求是日期类型或日期格式的字符串类型。输入holidays时有效且必选。节假日时间列不可以包含空值。日期格式样例：2021-01-01 00:00:00。	无

使用示例

1. 构建算子结构，配置参数，完成训练。

   

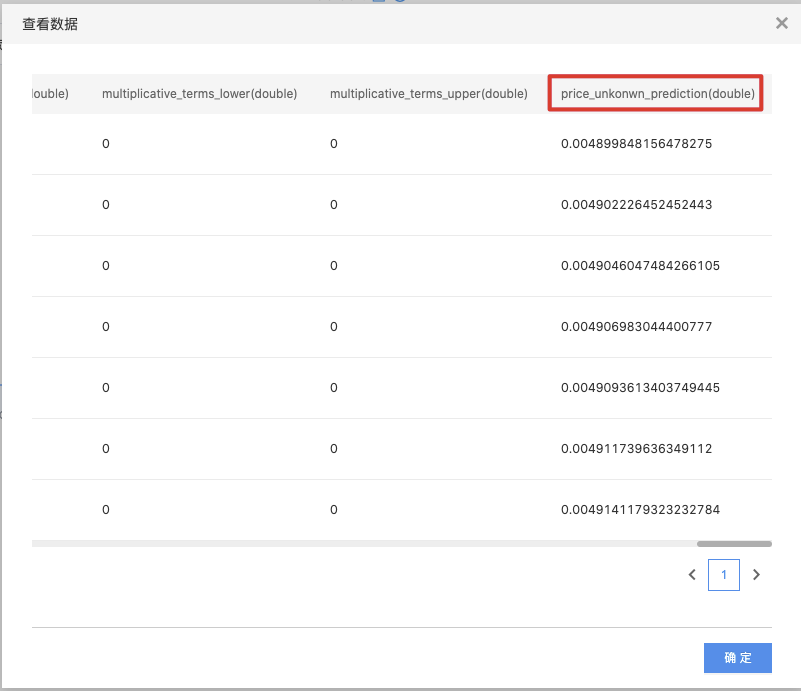
2. 右键“Prophet"组件，选择“查看数据” > "输出数据集"，查看输出结果。

   以”_prediction“结尾的列为预测结果列。