006-回归算法
回归算法
DecisionTree回归
决策树(DecisionTree)回归是基于回归树的决策树模型。一个回归树对应着输入空间(特征空间)的一个划分以及在划分单元上的输出值。输入空间的划分是通过遍历所有输入变量,找到最优的切分变量和最优的切分点,将输入空间划分为两部分,然后重复这个操作得到;划分单元上的输出值是该单元内所有样本点的均值。 划分度量使用均方误差的方法。
输入
- 输入一个数据集,数据集的特征列是数值或数组类型,标记列是数值类型。
输出
- 输出DecisionTree回归模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 树最大深度 | 是 | 决策树最大深度 范围:[0, 30]。 | 5 |
| 连续特征分箱 | 是 | 决策树连续特征分箱数 范围:[2, inf)。 | 32 |
| 最小信息增益 | 是 | 决策树分裂时最小信息增益 范围:[0.0, inf)。 | 0 |
| 节点最小样本数 | 是 | 决策树节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf)。 | 5 |
| 随机种子 | 否 | 随机种子 | 5 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求是数值类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| 树最大深度 | 是 | 决策树最大深度 范围:[0, 30]。 | 5 |
| 连续特征分箱数 | 是 | 决策树连续特征分箱数 范围:[2, inf)。 | 32 |
| 节点最小样本数 | 是 | 决策树节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf)。 | 5 |
| 最小信息增益 | 是 | 决策树分裂时最小信息增益 范围:[0.0, inf)。 | 0 |
| 评估标准 | 是 | 选择评估标准: 平均绝对误差 平均绝对百分误差 均方误差 判定系数 均方根误差 |
均方误差 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
评估方法
下列公式中:

平均绝对误差:它表示预测值和观测值之间绝对误差的平均值。
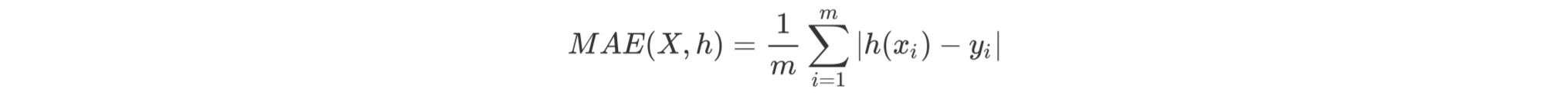
平均绝对百分误差:它是一个百分比值,因此比其他统计量更容易理解。例如,如果 MAPE 为 5,则表示预测结果较真实结果平均偏离5%。
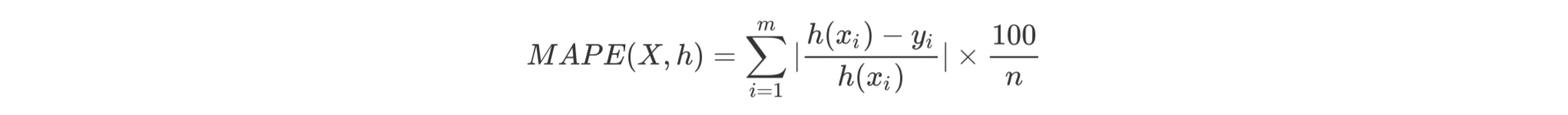
均方误差:表示预测数据和原始数据对应点误差的平方和的均值
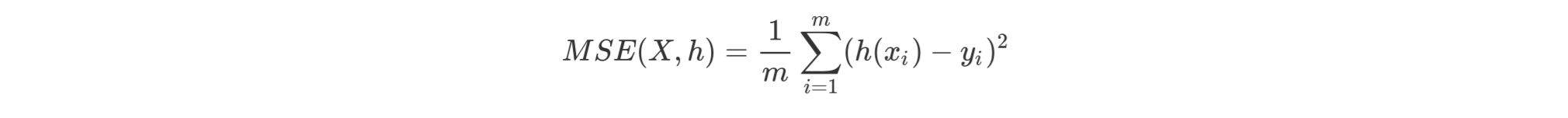
判定系数:用于估计回归方程是否很好的拟合了样本的数据,判定系数为估计的回归方程提供了一个拟合优度的度量。
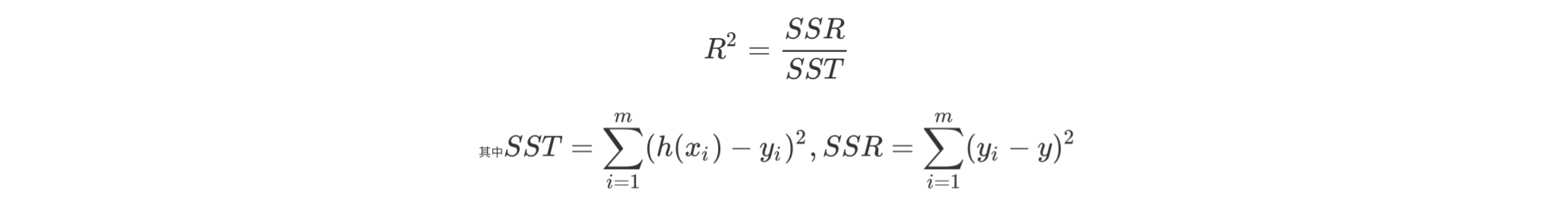
均方根误差:表示预测值和观测值之间差异(称为残差)的样本标准差。均方根误差为了说明样本的离散程度。做非线性拟合时,RMSE越小越好。
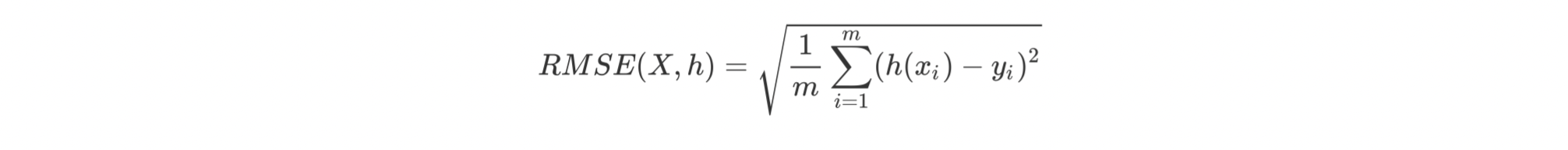
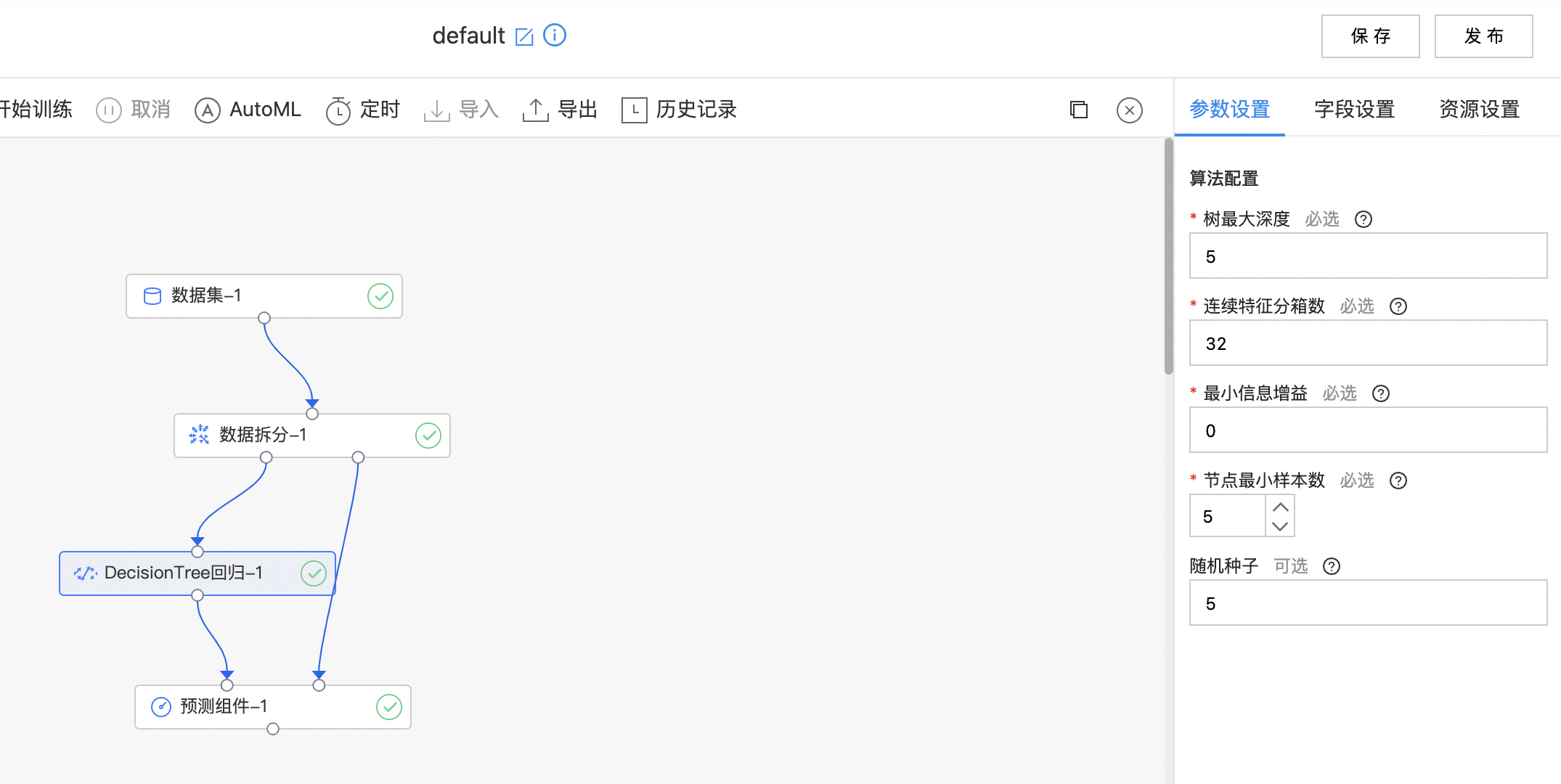
使用示例
1.构建算子结构,配置参数,完成训练。
GBDT回归
GBDT是一种迭代的决策树算法,该算法由多棵决策树组成,所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。GBDT中的树是回归树(不是分类树),GBDT用来做回归预测,调整后也可以用于分类。
输入
- 输入一个数据集,数据集的特征列是数值或数组类型,标记列是数值类型。
输出
- 输出GBDT回归模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 损失函数 | 是 | 最小化损失函数,支持 "squared" (L2) 和 "absolute" (L1)。 | squared |
| 树的最大深度 | 是 | GBDT中树(基学习器)的最大深度 范围:[0, inf)。 | 5 |
| 连续特征分箱数 | 是 | 连续特征的最大分箱数 范围:[2, inf)。 | 32 |
| 节点最小样本数 | 是 | GBDT中树(基学习器)的节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf)。 | 1 |
| 最小信息增益 | 是 | GBDT中树(基学习器)分裂时最小信息增益 范围:[0.0, inf) | 0 |
| 训练集学习器选取训练数据集的百分比 | 是 | 每次迭代训练基学习器时所使用的训练数据集的百分比 范围:[1.0E-15, 1.0]。 | 1 |
| 学习率 | 是 | 学习率,用于缩小(shrinking)每个基学习器的贡献 范围:[1.0E-15, 1.0]。 | 0.1 |
| 最大迭代轮数 | 是 | 当迭代次数大于该数值时,停止迭代 范围:[1, 200]。 | 100 |
| 随机种子 | 否 | 随机种子 | 5 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求是数值类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| 树的最大深度 | GBDT中树(基学习器)的最大深度 范围:[0, inf)。 | 5 | |
| 连续特征分箱数 | 连续特征的最大分箱数 范围:[2, inf)。 | 32 | |
| 节点最小样本数 | GBDT中树(基学习器)的节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分 范围:[1, inf)。 | 1 | |
| 最小信息增益 | GBDT中树(基学习器)分裂时最小信息增益 范围:[0.0, inf) | 0 | |
| 训练集学习器选取训练数据集的百分比 | 每次迭代训练基学习器时所使用的训练数据集的百分比 范围:[1.0E-15, 1.0]。 | 1 | |
| 学习率 | 学习率,用于缩小(shrinking)每个基学习器的贡献 范围:[1.0E-15, 1.0]。 | 0.1 | |
| 最大迭代轮数 | 当迭代次数大于该数值时,停止迭代 范围:[1, 200]。 | 100 | |
| 评估标准 | 是 | 选择评估标准: 平均绝对误差 平均绝对百分误差 均方误差 判定系数 均方根误差 |
均方误差 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
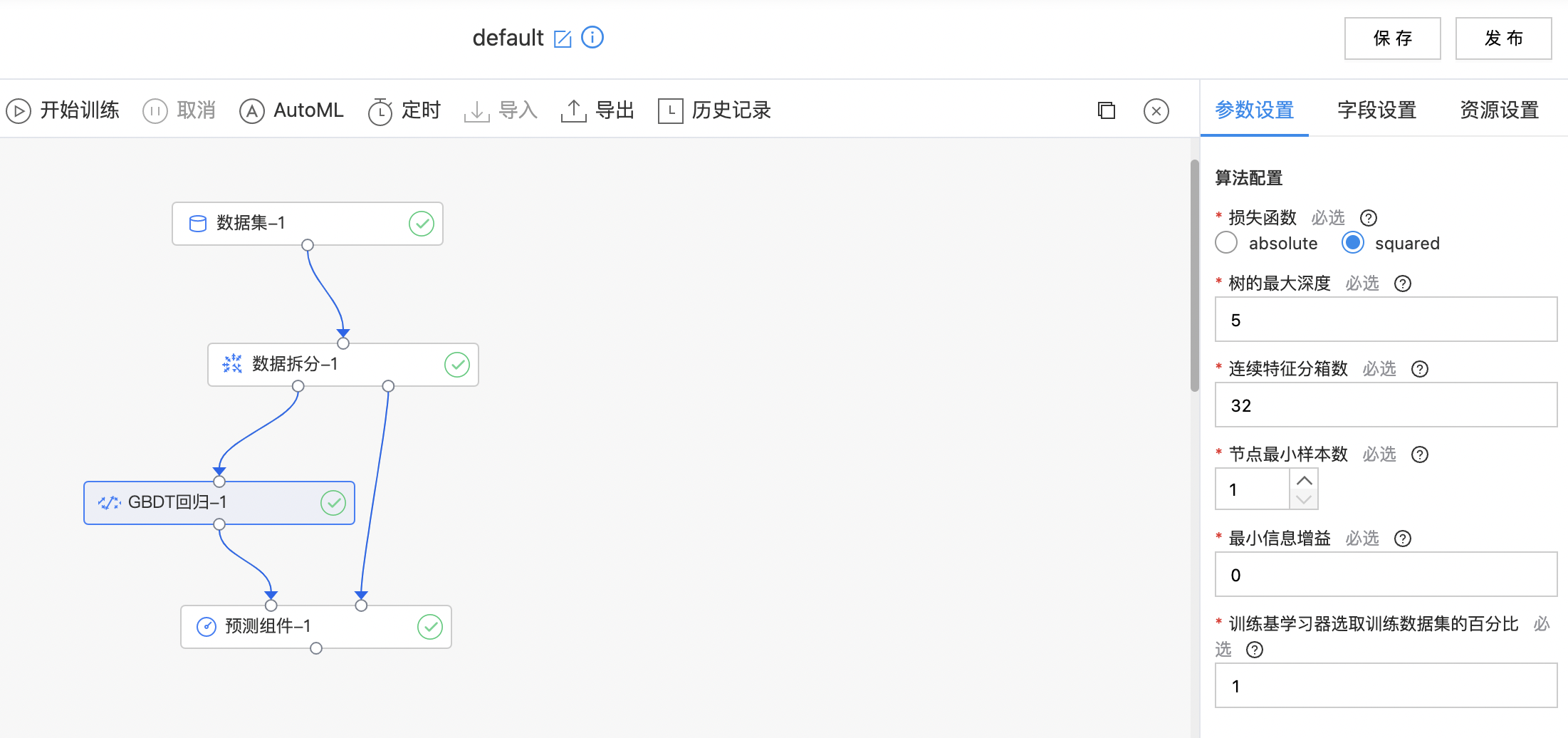
使用示例
构建算子结构,配置参数,完成训练。
广义线性回归
广义线性模型 (generalized linear model) 是在普通线性模型的基础上推广而得出的应用范围更广,更具实用性的回归模型。
输入
- 输入一个数据集,数据集的特征列是数值或数组类型,标记列是数值类型。
输出
- 输出广义线性回归模型,误差分布类型为twrrdie时不支持pmml导出。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 误差分布类型 | 是 | 误差分布类型,只有误差分布类型为tweedie时支持标签列含负数(不支持导出为Pmml模型),分布类型为binomial时标签列的值应在[0,1]之间,目前支持分布类型: binomial gamma gaussian tweedie poisson |
gaussian |
| 连接函数 | 是 | 连接函数,描述线性预测器和分布函数均值之间的关系,目前支持:logit cloglog probit identity inverse log sqrt |
identity |
| 方差函数中的幂 | 是 | 方差函数中的幂表示方差与分布均值之间的关系,支持的值为0和[1,inf),当值为0、1或2分别对应Gaussian, Poisson or Gamma Family 范围:[0.0, inf) | 0.0 |
| 连接参数 | 否 | 当值为0, 1, -1 或 0.5时,分别对应Log, Identity, Inverse 或 Sqrt 连接 | 无 |
| 截距 | 是 | 是否开启截距 | 开启 |
| 正则化参数 | 是 | L2正则化的正则化参数 范围:[0.0, inf) | 0.0 |
| 最大迭代轮数 | 是 | 当迭代次数大于该数值时,停止迭代 范围:[1, 200] | 25 |
| 目标收敛阈值 | 是 | 两次迭代之间的这个值小于阈值则停止训练 范围:[0.0, inf) | 1e-6 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求是数值类型,只有误差分布类型为tweedie时支持标签列含负数。 | 无 |
计算逻辑
广义线性模型可以定义为:

响应变量的分布推广至指数分散族 (exponential dispersion family):比如泊松分布、二项分布、伽玛分布、高斯分布等。
使用示例
构建算子结构,配置参数,完成训练。
线性回归
线性回归是分析因变量和多个自变量之间线性关系的模型。它试图学得一个线性模型以尽可能准确地预测实值输出标记。
输入
- 输入一个数据集,数据集的特征列是数值或数组类型,标记列是数值类型。
输出
- 输出线性回归模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| alpha | 是 | 正则项的选择,alpha=0代表L2正则,alpha=1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0]。 | 0.00 |
| lambda | 是 | 正则项的系数,0代表没有正则,越大代表正则强度越大 范围:[0.0, 2.0] | 1 |
| 随机种子 | 否 | 随机种子 | 无 |
| 最大迭代轮数 | 否 | 最大迭代轮数 范围:[1, 1000] | 20 |
| 目标收敛阈值 | 否 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练。默认值1e-6 范围:[1.0E-15, 0.999999999999999] | 1e-6 |
| 是否交叉验证 | 是 | 是否进行交叉验证 | 否 |
| 交叉分数 | 是 | 交叉验证的份数 范围:[2, 20] | 5 |
| 交叉验证划分方式 | 是 | 交叉验证每份的划分方式。选择分层划分的话,是按照分类目标列分层划分。目前支持:取余划分和随机划分。 | 随机划分 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求是数值类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| alpha | 是 | 正则项的选择,alpha=0代表L2正则,alpha=1代表L1正则,取中间值代表二者的线性组合 范围:[0.0, 1.0]。 | 0 |
| lambda | 是 | 正则项的系数,0代表没有正则,越大代表正则强度越大 范围:[0.0, 2.0]。 | 1 |
| 最大迭代轮数 | 是 | 最大迭代轮数 范围:[1, 1000] 。 | 20 |
| 目标收敛阈值 | 是 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练。默认值1e-6 范围:[1.0E-15, 0.999999999999999]。 | 1e-6 |
| 评估标准 | 是 | 选择评估标准: 平均绝对误差 平均绝对百分误差 均方误差 判定系数 均方根误差 |
均方误差 |
| 保存模型数量 | 是 | 保存模型的数量 | 1 |
计算逻辑
线性回归模型:
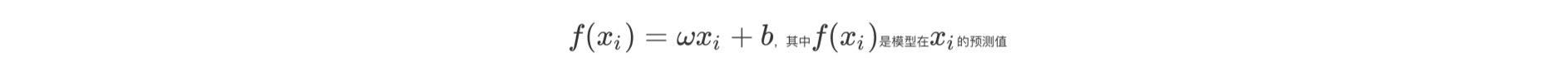
损失函数通过最小化训练样本到模型的距离,进而迭代出最优模型参数。
使用示例
构建算子结构,配置参数,完成训练。
随机森林回归
随机森林回归是基于随机森林且对应于回归任务的回归模型。原理与分类一致。基学习器为 DecisionTree 回归。结合策略是使用平均法。
输入
- 输入一个数据集,数据集的特征列是数值或数组类型,标记列是数值类型。
输出
- 输出随机森林回归模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征采样策略 | 是 | 选择特征采样: 所有特征 自动选择 总特征树以二为底的对数 定值 三分之一的特征 总特征数的一定比例 总特证数的平方根 |
自动选择 |
| 特征采样数 | 是 | 每次分裂子树时,考虑多少个特征 范围:[1, inf)。 | 10 |
| 比例 | 是 | 每次分裂子树时,考虑的特征数占总特征数的比例 范围:[0.001, 0.999]。 | 0.632 |
| 树的最大深度 | 是 | 子树的最大深度,范围:[2, 30]。 | 5 |
| 最小信息增益 | 是 | 每次分裂所需的最小信息增益 范围:[0.0, inf)。 | 0.0 |
| 节点最小样本数 | 是 | 随机森林中树的节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分,范围:[1, inf)。 | 1 |
| 树的数量 | 是 | 树的数量,范围:[1, inf)。 | 20 |
| 随机种子 | 是 | 随机种子 | 1 |
| 采样率 | 是 | 训练每个子树时,使用的样本占总样本的比例。采样率不宜过小,至少应当保证(训练样本数*采样率>1),否则训练出的模型在预测时会报错 Can not normalize the 0-vector. 范围:[0.001, 0.999]。 | 0.632 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求是数值类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| 树的最大深度 | 是 | 子树的最大深度,范围:[2, 30]。 | 5 |
| 最小信息增益 | 是 | 每次分裂所需的最小信息增益 范围:[0.0, inf)。 | 0.0 |
| 节点最小样本数 | 是 | 随机森林中树的节点最小样本数,当拆分节点后子节点中样本数量小于最小样本数时,该节点不进行拆分,范围:[1, inf)。 | 1 |
| 树的数量 | 是 | 树的数量,范围:[1, inf)。 | 20 |
| 采样率 | 是 | 训练每个子树时,使用的样本占总样本的比例。采样率不宜过小,至少应当保证(训练样本数*采样率>1),否则训练出的模型在预测时会报错 Can not normalize the 0-vector. 范围:[0.001, 0.999]。 | 0.632 |
| 评估标准 | 是 | 选择评估标准: 平均绝对误差 平均绝对百分误差 均方误差 判定系数 均方根误差 |
均方误差 |
| 保存模型数量 | 是 | 保存模型的数量。 | 1 |
使用示例
构建算子结构,配置参数,完成训练。
岭回归
岭回归可以被看作为一种改良后的最小二乘法,它通过向损失中添加L2正则项有效防止模型出现过拟合,且有助于解决非满秩条件下求逆困难的问题,从而提升模型的解释能力。
输入
- 输入一个数据集,数据集的特征列是数值或数组类型,标记列是数值类型。
输出
- 输出岭回归模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| lambda | 是 | 正则项的系数,0代表没有正则,越大代表正则强度越大 范围:[0.0, 2.0]。 | 1 |
| 随机种子 | 否 | 随机种子,用于保证多次训练结果相同。 | 无 |
| 最大迭代轮数 | 否 | 最大迭代轮数 范围:[1, 1000]。 | 20 |
| 目标收敛阈值 | 否 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练。默认值1e-6 范围:[1.0E-15, 0.999999999999999]。 | 1e-6 |
| 是否交叉验证 | 是 | 是否进行交叉验证 | 否 |
| 交叉份数 | 是 | 交叉验证的份数 范围:[2, 20]。 | 5 |
| 交叉验证划分方式 | 是 | 交叉验证每份的划分方式。选择分层划分的话,是按照分类目标列分层划分。目前支持取余划分和随机划分。 | 随机划分 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。 | 无 |
| 标签列 | 是 | 预测目标列,要求是数值类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| lambda | 是 | 正则项的系数,0代表没有正则,越大代表正则强度越大 范围:[0.0, 2.0]。 | 1 |
| 最大迭代轮数 | 是 | 最大迭代轮数 范围:[1, 1000]。 | 20 |
| 目标收敛阈值 | 是 | 计算方式(old_val - new_val)/old_val。两次迭代之间的这个值小于阈值则停止训练。默认值1e-6 范围:[1.0E-15, 0.999999999999999]。 | 1e-6 |
| 评估标准 | 是 | 选择评估标准: 平均绝对误差 平均绝对百分误差 均方误差 判定系数 均方根误差 |
均方误差 |
| 保存模型数量 | 是 | 保存模型的数量。 | 1 |
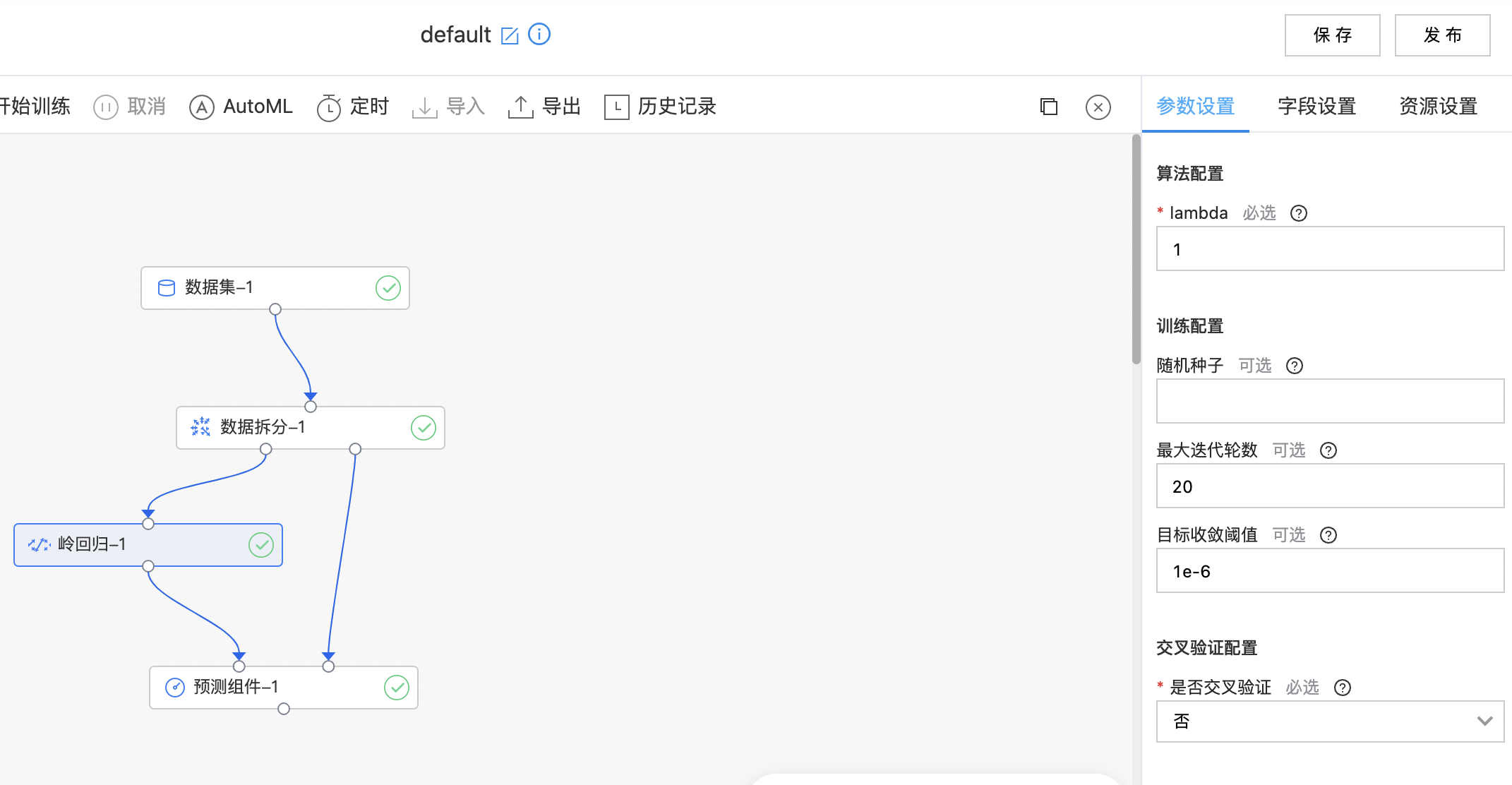
使用示例
构建算子结构,配置参数,完成训练。
XGBoost回归
XGBoost 是一种迭代的决策树算法,它是由多棵决策树组成,所有树的结论累加起来做最终答案。XGBoost 几乎可用于所有回归问题(线性/非线性)。
输入
- 输入一个数据集,数据集的特征列是数值或数组类型,标记列是数值类型。
输出
- 输出XGBoost回归模型。
算子参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 目标函数 | 是 | 待优化的目标函数,如果选择reg:logistic,标签列只能在0到1之间。目前支持: reg:gamma reg:logistic reg:squarederror reg:tweedie |
reg:squarederror |
| 评估指标 | 是 | 选择评价指标: rmse mae |
rmse |
| 树最大深度 | 是 | xgboost中每棵树的最大深度,树越深通常模型越复杂,更容易过拟合。 范围:[1, inf) | 6 |
| 迭代次数 | 是 | xgboost迭代次数 范围:[1, 200]。 | 5 |
| 最小叶子节点样本权重和 | 是 | 叶子结点需要的最小样本权重和 范围:[0.0, inf)。 | 1 |
| 正负样本比例 | 是 | 正负样本比例 范围:[1.0E-8, inf)。 | 1 |
| 学习率 | 是 | 学习率 范围:[0.0, 1.0]。 | 0.30 |
| gamma | 是 | 节点分裂所需的最小损失函数下降值 范围:[0.0, inf)。 | 0 |
| 随机采样比例 | 是 | 构造每棵树的所用样本比例(样本采样比例) 范围:[0.01, 1.0]。 | 1.00 |
| 随机采样的特正比例 | 是 | 构造每棵树的所用特征比例 范围:[0.01, 1.0]。 | 1.00 |
| L1正则化系数 | 是 | L1正则化系数 范围:[0.0, inf)。 | 0 |
| L2正则化系数 | 是 | L2正则化系数 范围:[0.0, inf)。 | 1 |
| 随机种子 | 是 | 随机种子 | 0 |
| UseExternalMemory | 是 | 是否使用ExternalMemory | 开启 |
字段参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 特征列 | 是 | 预测使用的特征列,要求必须是数值或数值数组类型。当数据量过大时,需增加内存。 | 无 |
| 标签列 | 是 | 预测标签列,要求是数值类型。 | 无 |
AutoML参数
| 参数名称 | 是否必选 | 参数描述 | 默认值 |
|---|---|---|---|
| 数据拆分比例 | 是 | 选择数据拆分比例,范围:[0.1,0.9]。 | 0.8 |
| 调参方式 | 是 | 选择调参方式: GridSearch RandomSearch |
GridSearch |
| 网格拆分数 | 是 | 选择网格拆分数,范围:[2,10]。 | 5 |
| 参数总组数 | 是 | 选择参数总组数,范围:[2,10]。 | 5 |
| 树最大深度 | 是 | xgboost中每棵树的最大深度,树越深通常模型越复杂,更容易过拟合。 范围:[1, inf) | 6 |
| 迭代次数 | 是 | xgboost迭代次数 范围:[1, 200]。 | 5 |
| 最小叶子节点样本权重和 | 是 | 叶子结点需要的最小样本权重和 范围:[0.0, inf)。 | 1 |
| 学习率 | 是 | 学习率 范围:[0.0, 1.0]。 | 0.3 |
| gamma | 是 | 节点分裂所需的最小损失函数下降值 范围:[0.0, inf)。 | 0 |
| L1正则化系数 | 是 | L1正则化系数 范围:[0.0, inf)。 | 0 |
| L2正则化系数 | 是 | L2正则化系数 范围:[0.0, inf)。 | 1 |
| 评估标准 | 是 | 选择评估标准: 平均绝对误差 平均绝对百分误差 均方误差 判定系数 均方根误差 |
均方误差 |
| 保存模型数量 | 是 | 保存模型的数量。 | 1 |
使用示例
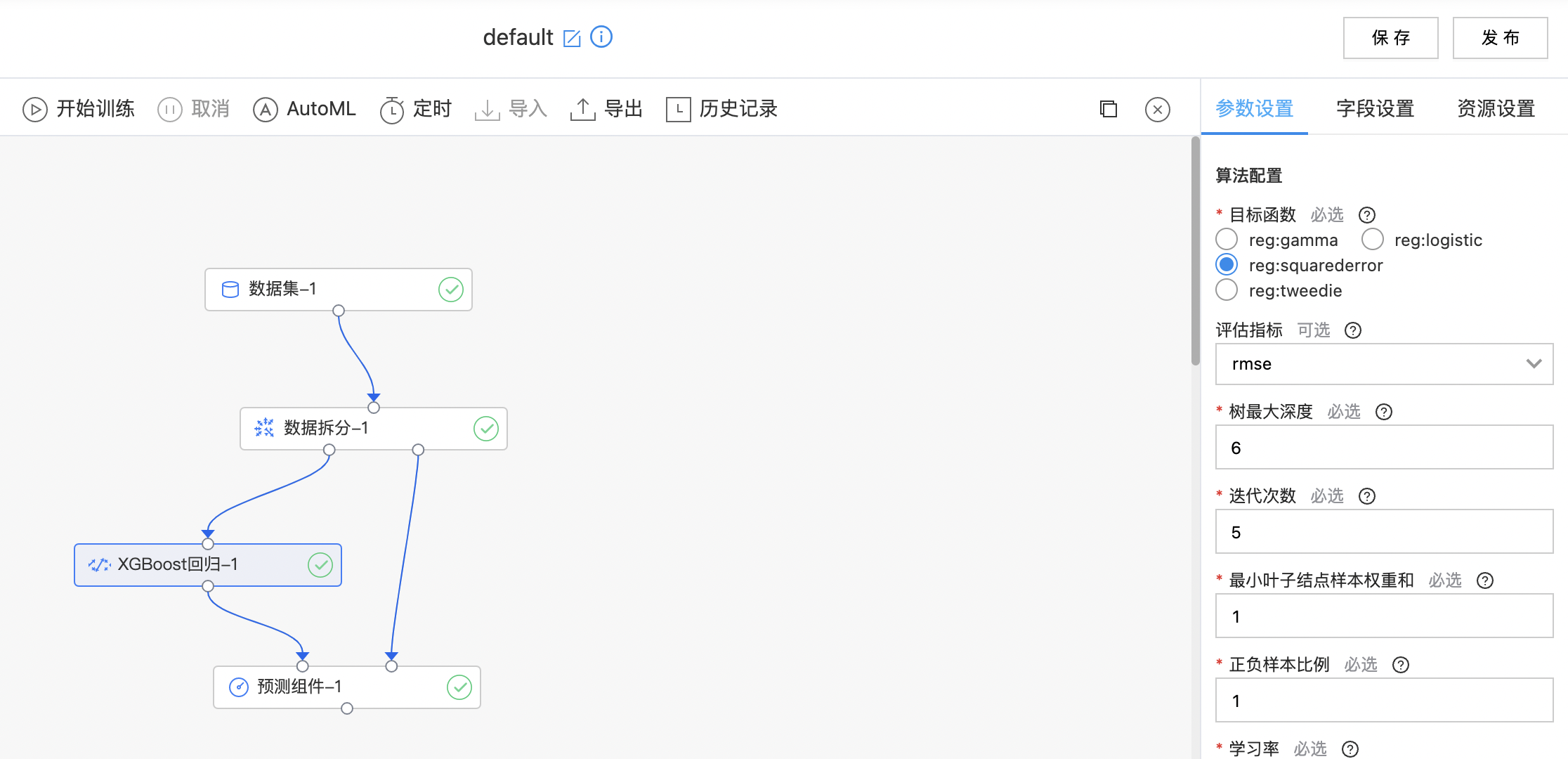
构建算子结构,配置参数,完成训练,算子支持查看全量特征重要性。